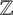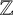1 results
THE LIFTING PROBLEM FOR UNIVERSAL QUADRATIC FORMS OVER SIMPLEST CUBIC FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 77-89
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
-
The lifting problem for universal quadratic forms over a totally real number field K consists of determining the existence or otherwise of a quadratic form with integer coefficients (or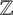
$\mathbb {Z}$-form) that is universal over K. We prove the nonexistence of universal 
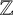$\mathbb {Z}$-forms over simplest cubic fields for which the integer parameter is big enough. The monogenic case is already known. We prove the nonexistence in the nonmonogenic case by using the existence of a totally positive nonunit algebraic integer in K with minimal (codifferent) trace equal to one.
