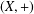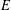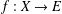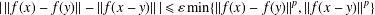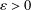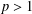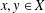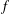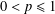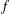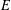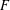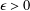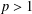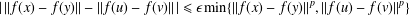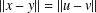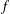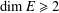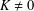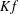1 results
ON HYPERSTABILITY OF ADDITIVE MAPPINGS ONTO BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 30 December 2014, pp. 278-285
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
-
Let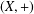
$(X,+)$ be an Abelian group and 
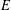$E$ be a Banach space. Suppose that 
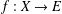$f:X\rightarrow E$ is a surjective map satisfying the inequality for some
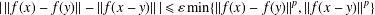$$\begin{eqnarray}|\,\Vert f(x)-f(y)\Vert -\Vert f(x-y)\Vert \,|\leq {\it\varepsilon}\min \{\Vert f(x)-f(y)\Vert ^{p},\Vert f(x-y)\Vert ^{p}\}\end{eqnarray}$$
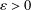${\it\varepsilon}>0$, 
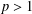$p>1$ and for all 
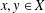$x,y\in X$. We prove that 
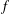$f$ is an additive map. However, this result does not hold for 
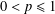$0<p\leq 1$. As an application, we show that if 
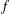$f$ is a surjective map from a Banach space 
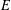$E$ onto a Banach space 
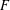$F$ so that for some 
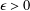${\it\epsilon}>0$ and 
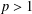$p>1$whenever
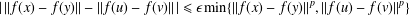$$\begin{eqnarray}|\,\Vert f(x)-f(y)\Vert -\Vert f(u)-f(v)\Vert \,|\leq {\it\epsilon}\min \{\Vert f(x)-f(y)\Vert ^{p},\Vert f(u)-f(v)\Vert ^{p}\}\end{eqnarray}$$
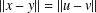$\Vert x-y\Vert =\Vert u-v\Vert$, then 
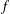$f$ preserves equality of distance. Moreover, if 
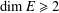$\dim E\geq 2$, there exists a constant 
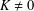$K\neq 0$ such that 
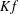$Kf$ is an affine isometry. This improves a result of Vogt [‘Maps which preserve equality of distance’, Studia Math.45 (1973) 43–48].
