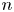Navigators have been taught for centuries to estimate the location of their craft on a map from three lines of position, for redundancy. The three lines typically form a triangle, called a cocked hat. How is the location of the craft related to the triangle? For more than 80 years navigators have also been taught that, if each line of position is equally likely to pass to the right and to the left of the true location, then the likelihood that the craft is in the triangle is exactly 1/4. This is stated in numerous reputable sources, but was never stated or proved in a mathematically formal and rigorous fashion. In this paper we prove that the likelihood is indeed 1/4 if we assume that the lines of position always intersect pairwise. We also show that the result does not hold under weaker (and more reasonable) assumptions, and we prove a generalisation to 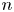$n$ lines.

A dual-axis rotational Inertial Navigation System (INS) has received wide attention in recent years because of high performance and low cost. However, some errors of inertial sensors such as stochastic errors are not averaged out automatically during navigation. Therefore a Twice Position-fix Reset (TPR) method is provided to enhance accuracy of a dual-axis rotational INS by compensating stochastic errors. According to characteristics of an azimuth error introduced by stochastic errors of an inertial sensor in the dual-axis rotational INS, both an azimuth error and a radial-position error are much better corrected by the TPR method based on an optimised error propagation equation. As a result, accuracy of the dual-axis rotational INS is prominently enhanced by the TPR method, as is verified by simulations and field tests.