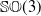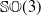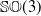Descriptions of various subsets of 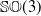 $\mathbb{SO}(3)$ are encountered frequently in robotics, for example, in the context of specifying the orientation workspaces of manipulators. Often, the Cartesian concept of a cuboid is extended into the domain of Euler angles, notwithstanding the fact that the physical implications of this practice are not documented. Motivated by this lacuna in the existing literature, this article focuses on studying sets of rotations described by such cuboids by mapping them to the space of Rodrigues parameters, where a physically meaningful measure of distance from the origin is available and the spherical geometry is intrinsically pertinent. It is established that the planar faces of the said cuboid transform into hyperboloids of one sheet and hence, the cuboid itself maps into a solid of complicated non-convex shape. To quantify the extents of these solids, the largest spheres contained within them are computed analytically. It is expected that this study would help in the process of design and path planning of spatial robots, especially those of parallel architecture, due to a better and quantitative understanding of their orientation workspaces.
$\mathbb{SO}(3)$ are encountered frequently in robotics, for example, in the context of specifying the orientation workspaces of manipulators. Often, the Cartesian concept of a cuboid is extended into the domain of Euler angles, notwithstanding the fact that the physical implications of this practice are not documented. Motivated by this lacuna in the existing literature, this article focuses on studying sets of rotations described by such cuboids by mapping them to the space of Rodrigues parameters, where a physically meaningful measure of distance from the origin is available and the spherical geometry is intrinsically pertinent. It is established that the planar faces of the said cuboid transform into hyperboloids of one sheet and hence, the cuboid itself maps into a solid of complicated non-convex shape. To quantify the extents of these solids, the largest spheres contained within them are computed analytically. It is expected that this study would help in the process of design and path planning of spatial robots, especially those of parallel architecture, due to a better and quantitative understanding of their orientation workspaces.
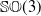 $\mathbb{SO}(3)$ towards describing subsets of
$\mathbb{SO}(3)$ towards describing subsets of 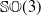 ${\mathbb{SO}}(3)$ geometrically and establishing the relations between these
${\mathbb{SO}}(3)$ geometrically and establishing the relations between these