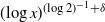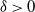We study generalizations of the forest fire model introduced in [4] and [10] by allowing the rates at which the trees grow to depend on their location, introducing long-range burning, as well as a continuous-space generalization of the model. We establish that in all the models in consideration the expected time required to reach a site at distance x from the origin is of order $(\!\log x)^{(\!\log 2)^{-1}+\delta}$ for any $\delta>0$ .

The concept of “self-organized criticality” (SOC) was originally proposed as an explanation of 1/f-noise by Bak, Tang, and Wiesenfeld (1987), but turned out to have a far broader significance for scale-free nonlinear energy dissipation processes occurring in the entire universe. Over the last 30 years, an inspiring cross-fertilization from complexity theory to solar and astrophysics took place, where the SOC concept was initially applied to solar flares, stellar flares, and magnetospheric substorms, and later extended to the radiation belt, the heliosphere, lunar craters, the asteroid belt, the Saturn ring, pulsar glitches, soft X-ray repeaters, blazars, black-hole objects, cosmic rays, and boson clouds. The application of SOC concepts has been performed by numerical cellular automaton simulations, by analytical calculations of statistical (powerlaw-like) distributions based on physical scaling laws, and by observational tests of theoretically predicted size distributions and waiting time distributions. Attempts have been undertaken to import physical models into numerical SOC toy models. The novel applications stimulated also vigorous debates about the discrimination between SOC-related and non-SOC processes, such as phase transitions, turbulence, random-walk diffusion, percolation, branching processes, network theory, chaos theory, fractality, multi-scale, and other complexity phenomena. We review SOC models applied to astrophysical observations, attempt to describe what physics can be captured by SOC models, and offer a critique of weaknesses and strengths in existing SOC models.

One of the most powerful SOC tools - the wavelet transform modulus maxima approach to calculating multifractality - is connected to one of the most powerful equations in all of physics - Ampere's law. In doing so, the multifractal spectra can be expressed in terms of current density, and how current density can then be used for the prediction of future energy release from such a system.

This paper uses daily observations for the Canadian dollar–U.S. dollar exchange rate over the recent flexible exchange-rate period (from January 2, 1974, to October 28, 2002), and various tests from dynamical systems theory, such as a chaos test, a self-organized criticality test, and a threshold effects test, to support a stochastic nonlinear origin for the series.

Uniform sequential tree-building aggregation of n particles is analyzed together with the effect of the avalanche that takes place when a subtree rooted at a uniformly chosen vertex is removed. For large n, the expected subtree size is found to be ≃ logn both for the tree of size n and the tree that remains after an avalanche. Repeated breakage-restoration cycles are seen to give independent avalanches which attain size k(1 ≤ k ≤ n-1) with probability (k(k+1))-1 and restored trees that are recursive.

The island of Minorca, Spain, has become a patchy mosaic landscape as a result of centuries of human-induced fragmentation. The dynamics of the landscape elements and the spatial pattern of Minorca were analysed to test whether this human-modelled landscape was at a stationary state, and, if it was the case, to see whether the system could be characterized by a particular spatial pattern. Landsat TM satellite images were processed to derive land cover classification and vegetation index maps corresponding to the years 1984 and 1992, the best compromise between null cloudiness and maximum time span. The classification was used to test the stationary state by estimating the transition matrix of land cover. The Normalized Difference Vegetation Index (NDVI) was used to analyse the spatial pattern of change at the patch level. The spatial analysis of NDVI was based on four indices: fractal dimension, number and size distribution of patches, and spatial Kappa index. Those pattern descriptors were compared with values obtained from stochastic landscape simulations. Temporal analysis showed that land cover proportions remained approximately constant over the 8-year period, although interchange amongst patches existed. This suggested that the landscape of Minorca was close to a stationary state. The study of NDVI changes revealed that the spatial structure was different from that of neutral models and presented scale invariance properties. Results from land cover transitions and from NDVI patterning suggest that the landscape of Minorca is a critical system, in the framework of the self-organized criticality hypothesis, i.e. the mosaic of patches would self-organize at the frontier of a dynamic equilibrium constituted by the balance between disturbances and successional processes.