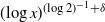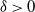1. Introduction
The purpose of this paper is to generalize the results for the version of the forest fire model studied in [Reference Volkov10]; see also [Reference van den Berg and Tóth4] and [Reference Crane, Freeman and Tóth6]. In that model, one considers the following continuous-time process on
![]() $\mathbb{Z}_+=\{0,1,2,\ldots\}$
. Let
$\mathbb{Z}_+=\{0,1,2,\ldots\}$
. Let
![]() $\eta_x(t)\in \{0,1\}$
be the state of site
$\eta_x(t)\in \{0,1\}$
be the state of site
![]() $x\in \mathbb{Z}_+$
at time
$x\in \mathbb{Z}_+$
at time
![]() $t\ge 0$
. Site x is declared vacant (resp. occupied) if
$t\ge 0$
. Site x is declared vacant (resp. occupied) if
![]() $\eta_x=0$
(resp.
$\eta_x=0$
(resp.
![]() $\eta_x=1$
) The process evolves as follows: vacant sites become occupied independently with rate 1; after they are occupied, they can be ‘burnt’ by a fire spread from a neighbour on the left, which makes them vacant again. There is a constant (and the only) source of fire attached to site 0; so when site 0 becomes occupied, the whole connected cluster of occupied sites which contains 0 is instantaneously burnt out.
$\eta_x=1$
) The process evolves as follows: vacant sites become occupied independently with rate 1; after they are occupied, they can be ‘burnt’ by a fire spread from a neighbour on the left, which makes them vacant again. There is a constant (and the only) source of fire attached to site 0; so when site 0 becomes occupied, the whole connected cluster of occupied sites which contains 0 is instantaneously burnt out.
Initially all the sites are vacant. We are interested in the dynamics of process
![]() $\{\eta_x(t)\}$
as
$\{\eta_x(t)\}$
as
![]() $t\to\infty$
. For other relevant models of forest fires we refer the reader to [Reference van den Berg and Brouwer2], [Reference van den Berg and Járai3], and [Reference Bressaud and Fournier5]; also, some more recent results dealing with complete graphs can be found in [Reference Crane, Freeman and Tóth6] and for planar lattices in [Reference Kiss, Manolescu and Sidoravicius8]. See also [Reference Martin and Ráth9] for the connection between the multiplicative coalescent with linear deletion and forest fires.
$t\to\infty$
. For other relevant models of forest fires we refer the reader to [Reference van den Berg and Brouwer2], [Reference van den Berg and Járai3], and [Reference Bressaud and Fournier5]; also, some more recent results dealing with complete graphs can be found in [Reference Crane, Freeman and Tóth6] and for planar lattices in [Reference Kiss, Manolescu and Sidoravicius8]. See also [Reference Martin and Ráth9] for the connection between the multiplicative coalescent with linear deletion and forest fires.
In this paper we consider the following two generalizations.
-
(i) We allow the rates at which vacant site x becomes occupied to depend on x, though they all must lie in a certain interval, and also consider a long-range mode (the terminology is consistent with use in the percolation theory), where the fires can spread further than just to the immediate neighbour of the ‘burning’ site.
Note that for each site x the sequence of burning times at x is a renewal process that is measurable with respect to the filtration generated by the arrival processes at the sites
 $\{0,1,\ldots,x\}$
.
$\{0,1,\ldots,x\}$
.The results are presented in Theorem 1 below.
-
(ii) We also consider a continuous-space generalization of the process where we replace
 $\mathbb{Z}_+$
with
$\mathbb{Z}_+$
with
 $\mathbb{R}_+$
; the main result here is our Theorem 2. We want to mention that in this case we consider only a homogeneous version, as even then the arguments become quite complicated.
$\mathbb{R}_+$
; the main result here is our Theorem 2. We want to mention that in this case we consider only a homogeneous version, as even then the arguments become quite complicated.
We note that the bounds on the expected time to reach point x given by Theorems 1 and 2 are probably suboptimal; we expect them in reality to be of order
![]() $\log x$
(as was shown for a simpler model in [Reference Volkov10]) rather than some power of
$\log x$
(as was shown for a simpler model in [Reference Volkov10]) rather than some power of
![]() $\log x$
; however, we do not see how to prove it in a general case.
$\log x$
; however, we do not see how to prove it in a general case.
The rest of the paper is organized as follows. In Section 2 we present the formal definition of the processes we study. In Section 3 we formulate and prove our main theorem for model (i). The strategy of the proof is roughly as follows. First we introduce an auxiliary ‘green’ process, which is a version of the forest process without fires, and we study how far a potential fire could reach, should it occur at the specific point of time. It turns out that it is much easier to study this auxiliary process, and at the same time the ‘real’ fire process and the green process coincide from time to time. This allows us to introduce an increasing sequence of locations
![]() $n_k\uparrow \infty$
, and using intricate coupling to get an upper bound of the expected time when the
$n_k\uparrow \infty$
, and using intricate coupling to get an upper bound of the expected time when the
![]() $n_k$
are burned for the first time. Finally, in Section 4 we formulate and prove the theorem about the continuous version of the model.
$n_k$
are burned for the first time. Finally, in Section 4 we formulate and prove the theorem about the continuous version of the model.
Throughout the paper we will use notation
![]() $a(t)\asymp b(t)$
if
$a(t)\asymp b(t)$
if
![]() $\lim_{t\to\infty} a(t)/b(t)=1$
, and we assume that all the processes are càdlàg, that is, at the time of the fire all points of the burning cluster become vacant.
$\lim_{t\to\infty} a(t)/b(t)=1$
, and we assume that all the processes are càdlàg, that is, at the time of the fire all points of the burning cluster become vacant.
2. Formal definitions and the ‘green’ process
The probability space on which we define the processes is as follows. Given a deterministic sequence
![]() $\{{\lambda}_x\}_{x\in\mathbb{Z}_+}$
, for each x we have an independent Poisson process of rate
$\{{\lambda}_x\}_{x\in\mathbb{Z}_+}$
, for each x we have an independent Poisson process of rate
![]() ${\lambda}_x$
, denoted by
${\lambda}_x$
, denoted by
![]() ${\mathcal{P}}_x(t)$
, started at zero. The probability and expectations throughout the paper will be with respect to the product measure generated by these processes; elementary outcomes will be denoted by
${\mathcal{P}}_x(t)$
, started at zero. The probability and expectations throughout the paper will be with respect to the product measure generated by these processes; elementary outcomes will be denoted by
![]() ${\omega}$
. Note that this definition will be slightly modified for model (ii).
${\omega}$
. Note that this definition will be slightly modified for model (ii).
The green process for the forest fire process
Consider the following modification of the forest fire process. Fix an
![]() $x\in\{1,2,\ldots\}$
. Assume that there are no fires at all, and wait for the first time when x is reachable from 0 (precisely defined immediately after (1)). This will provide a trivial lower bound for the minimum time necessary for the fire to reach this point.
$x\in\{1,2,\ldots\}$
. Assume that there are no fires at all, and wait for the first time when x is reachable from 0 (precisely defined immediately after (1)). This will provide a trivial lower bound for the minimum time necessary for the fire to reach this point.
More formally, let
![]() ${\mathcal{P}}_x$
,
${\mathcal{P}}_x$
,
![]() $x\in \mathbb{Z}_+$
, be a collection of independent Poisson processes, such that
$x\in \mathbb{Z}_+$
, be a collection of independent Poisson processes, such that
![]() ${\mathcal{P}}_x$
has rate
${\mathcal{P}}_x$
has rate
![]() ${\lambda}_x$
. Define a
${\lambda}_x$
. Define a
![]() $\{0,1\}^{\mathbb{Z}_+}$
-valued continuous-time stochastic process
$\{0,1\}^{\mathbb{Z}_+}$
-valued continuous-time stochastic process
![]() $S^{\color{ForestGreen}{\textbf{G}}}$
as follows. The value
$S^{\color{ForestGreen}{\textbf{G}}}$
as follows. The value
![]() $S^{\color{ForestGreen}{\textbf{G}}}(x,t)\in\{0,1\}$
for
$S^{\color{ForestGreen}{\textbf{G}}}(x,t)\in\{0,1\}$
for
![]() $x\in \mathbb{Z}+$
,
$x\in \mathbb{Z}+$
,
![]() $t\ge 0$
, is the state of site x at time t. We say that x is occupied at time t (resp. vacant) whenever
$t\ge 0$
, is the state of site x at time t. We say that x is occupied at time t (resp. vacant) whenever
![]() $S^{\color{ForestGreen}{\textbf{G}}}(x,t)=1$
(resp.
$S^{\color{ForestGreen}{\textbf{G}}}(x,t)=1$
(resp.
![]() $S^{\color{ForestGreen}{\textbf{G}}}(x,t)=0$
). At time
$S^{\color{ForestGreen}{\textbf{G}}}(x,t)=0$
). At time
![]() $t=0$
all the states are vacant, i.e.
$t=0$
all the states are vacant, i.e.
![]() $S^{\color{ForestGreen}{\textbf{G}}}(x,0)=0$
for all
$S^{\color{ForestGreen}{\textbf{G}}}(x,0)=0$
for all
![]() $x\ge 0$
.
$x\ge 0$
.
At each arrival time of the Poisson process
![]() ${\mathcal{P}}_x$
, the state x becomes 1, regardless of its previous value. Formally,
${\mathcal{P}}_x$
, the state x becomes 1, regardless of its previous value. Formally,
 \begin{align}S^{\color{ForestGreen}{\textbf{G}}}(x,t)=\begin{cases}0 &\text{if $ {\mathcal{P}}_x(t)=0$,}\\1 &\text{if $ {\mathcal{P}}_x(t)\ge 1$.}\end{cases}\end{align}
\begin{align}S^{\color{ForestGreen}{\textbf{G}}}(x,t)=\begin{cases}0 &\text{if $ {\mathcal{P}}_x(t)=0$,}\\1 &\text{if $ {\mathcal{P}}_x(t)\ge 1$.}\end{cases}\end{align}
Let
![]() $r\ge 1$
(called the range of the process) be some positive integer; we say that
$r\ge 1$
(called the range of the process) be some positive integer; we say that
![]() $x\in\{1,2,\ldots\}$
is reachable from 0 at time t if there exists a positive integer n and a sequence of points in
$x\in\{1,2,\ldots\}$
is reachable from 0 at time t if there exists a positive integer n and a sequence of points in
![]() $\mathbb{Z}_+$
$\mathbb{Z}_+$
![]() $0=x_0<x_1<x_2<\dots<x_n= x$
such that
$0=x_0<x_1<x_2<\dots<x_n= x$
such that
![]() $x_i-x_{i-1}\le r$
for
$x_i-x_{i-1}\le r$
for
![]() $i=1,2,\ldots,n$
and also
$i=1,2,\ldots,n$
and also
![]() $S^{\color{ForestGreen}{\textbf{G}}}(x_i,t)=1$
for
$S^{\color{ForestGreen}{\textbf{G}}}(x_i,t)=1$
for
![]() $i=0,1,2,\ldots,n-1$
(note that we do not require that
$i=0,1,2,\ldots,n-1$
(note that we do not require that
![]() $S^{\color{ForestGreen}{\textbf{G}}}(x,t)=1$
). This defines the green process. For the green process, we can define the quantity
$S^{\color{ForestGreen}{\textbf{G}}}(x,t)=1$
). This defines the green process. For the green process, we can define the quantity
![]() $N^{\color{ForestGreen}{\textbf{G}}}(t)$
, which is the rightmost reachable vertex at time t; in particular, if
$N^{\color{ForestGreen}{\textbf{G}}}(t)$
, which is the rightmost reachable vertex at time t; in particular, if
![]() $N^{\color{ForestGreen}{\textbf{G}}}(t)=n$
then
$N^{\color{ForestGreen}{\textbf{G}}}(t)=n$
then
![]() $S^{\color{ForestGreen}{\textbf{G}}}(n-r,t)=1$
and
$S^{\color{ForestGreen}{\textbf{G}}}(n-r,t)=1$
and
![]() $S^{\color{ForestGreen}{\textbf{G}}}(n-i,t)=0$
for
$S^{\color{ForestGreen}{\textbf{G}}}(n-i,t)=0$
for
![]() $i=0,1,\ldots,r-1$
. For definiteness, if
$i=0,1,\ldots,r-1$
. For definiteness, if
![]() $S^{\color{ForestGreen}{\textbf{G}}}(0,t)=0$
let
$S^{\color{ForestGreen}{\textbf{G}}}(0,t)=0$
let
![]() $N^{\color{ForestGreen}{\textbf{G}}}(t)=0$
.
$N^{\color{ForestGreen}{\textbf{G}}}(t)=0$
.
The time when point x becomes reachable for the first time is denoted by
It is easy to see that
![]() $N^{\color{ForestGreen}{\textbf{G}}}(t)<\infty$
a.s. and that
$N^{\color{ForestGreen}{\textbf{G}}}(t)<\infty$
a.s. and that
![]() $N^{\color{ForestGreen}{\textbf{G}}}(t)\uparrow\infty$
as
$N^{\color{ForestGreen}{\textbf{G}}}(t)\uparrow\infty$
as
![]() $t\to\infty$
a.s.
$t\to\infty$
a.s.
The forest fire process, denoted by
![]() $S^{\color{red}{\textbf{F}}}(x,t)$
, is easily defined on the same probability space generated by the same processes
$S^{\color{red}{\textbf{F}}}(x,t)$
, is easily defined on the same probability space generated by the same processes
![]() ${\mathcal{P}}_x(t)$
,
${\mathcal{P}}_x(t)$
,
![]() $x=0,1,2,\ldots,$
as the green process, with the additional rule saying that whenever site 0 becomes occupied, all the sites that are reachable from 0 become vacant. We say that all these sites are burnt at this time (regardless of whether or not they were previously occupied). Throughout the rest of the paper we let N(t) denote the rightmost point burnt by the fire by time t.
$x=0,1,2,\ldots,$
as the green process, with the additional rule saying that whenever site 0 becomes occupied, all the sites that are reachable from 0 become vacant. We say that all these sites are burnt at this time (regardless of whether or not they were previously occupied). Throughout the rest of the paper we let N(t) denote the rightmost point burnt by the fire by time t.
The previously studied case (e.g. in [Reference Volkov10]) when
![]() $r=1$
is referred to as the ‘short’ range, as opposed to the ‘long’ range when r can be greater than 1.
$r=1$
is referred to as the ‘short’ range, as opposed to the ‘long’ range when r can be greater than 1.
Remark 1. Suppose that
![]() ${\lambda}_x\equiv1$
and
${\lambda}_x\equiv1$
and
![]() $r=1$
as in [Reference Volkov10]. The process
$r=1$
as in [Reference Volkov10]. The process
![]() $N^{\color{ForestGreen}{\textbf{G}}}$
is then a time-inhomogeneous pure jump Markov process on
$N^{\color{ForestGreen}{\textbf{G}}}$
is then a time-inhomogeneous pure jump Markov process on
![]() $\mathbb{Z}_+$
with unit jump rate and with a
$\mathbb{Z}_+$
with unit jump rate and with a
![]() $\operatorname{Geom}\!({\mathrm{e}}^{-t})$
jump distribution, so
$\operatorname{Geom}\!({\mathrm{e}}^{-t})$
jump distribution, so
![]() $N^{\color{ForestGreen}{\textbf{G}}}(t)\,{\mathrm{e}}^{-t}$
converges in law to an exponential variable, and
$N^{\color{ForestGreen}{\textbf{G}}}(t)\,{\mathrm{e}}^{-t}$
converges in law to an exponential variable, and
 \begin{equation*}\mathbb{P}\bigl( N^{\color{ForestGreen}{\textbf{G}}}(t+{\mathrm{d}} t) =N^{\color{ForestGreen}{\textbf{G}}}(t)+k \mid {\text{history up to } \textit{t}}\bigr) =\begin{cases}1-{\mathrm{d}} t+{\mathrm{o}}({\mathrm{d}} t), & k=0, \\ {\mathrm{e}}^{-t}(1-{\mathrm{e}}^{-t})^{k-1} \,{\mathrm{d}} t + {\mathrm{o}}({\mathrm{d}} t),& k \geq 1. \end{cases}\end{equation*}
\begin{equation*}\mathbb{P}\bigl( N^{\color{ForestGreen}{\textbf{G}}}(t+{\mathrm{d}} t) =N^{\color{ForestGreen}{\textbf{G}}}(t)+k \mid {\text{history up to } \textit{t}}\bigr) =\begin{cases}1-{\mathrm{d}} t+{\mathrm{o}}({\mathrm{d}} t), & k=0, \\ {\mathrm{e}}^{-t}(1-{\mathrm{e}}^{-t})^{k-1} \,{\mathrm{d}} t + {\mathrm{o}}({\mathrm{d}} t),& k \geq 1. \end{cases}\end{equation*}
Indeed, for an individual site the probability of being occupied in time t is
![]() $1-{\mathrm{e}}^{-t}$
, and thus the longest stretch of such occupied sites has a geometric distribution. Since at time t we have
$1-{\mathrm{e}}^{-t}$
, and thus the longest stretch of such occupied sites has a geometric distribution. Since at time t we have
![]() $N^{\color{ForestGreen}{\textbf{G}}}(t)=n$
, the site
$N^{\color{ForestGreen}{\textbf{G}}}(t)=n$
, the site
![]() $n+1$
must be vacant at time t. If it becomes occupied during time
$n+1$
must be vacant at time t. If it becomes occupied during time
![]() ${\mathrm{d}} t$
, which occurs with probability
${\mathrm{d}} t$
, which occurs with probability
![]() ${\mathrm{d}} t$
, the process will immediately spread further to the right due to the already occupied sites at
${\mathrm{d}} t$
, the process will immediately spread further to the right due to the already occupied sites at
![]() $n+1,n+2,\ldots.$
$n+1,n+2,\ldots.$
The usefulness of the green process will become clear from Proposition 1, introduced later. At this point we outline our construction. The green and fire processes are naturally coupled: they have the same ‘reach’ at a sequence of times tending to infinity. The green process is a trivial upper bound for the other one, while it can be analysed somewhat explicitly. On the other hand, the fire process has enough of a renewal structure to estimate how much slower than the green process it can be.
Now we rigorously introduce models (i) and (ii) studied in the current paper.
(i) Non-homogeneous, long-range process
Suppose that the rate at which site x becomes occupied depends on the site, and denote it by
![]() ${\lambda}_x$
. Throughout the paper we will assume uniform bounds on these rates:
${\lambda}_x$
. Throughout the paper we will assume uniform bounds on these rates:
for some fixed constants
![]() $c_2>c_1>0$
. We will assume also that the process is long-range, that is, when the fire hits point x it burns all vertices in
$c_2>c_1>0$
. We will assume also that the process is long-range, that is, when the fire hits point x it burns all vertices in
![]() $[x,x+1,\ldots,x+r]$
for some fixed positive integer r (‘range’).
$[x,x+1,\ldots,x+r]$
for some fixed positive integer r (‘range’).
In the original model studied in [Reference Volkov10], one has
![]() ${\lambda}_x= 1$
for all x, and
${\lambda}_x= 1$
for all x, and
![]() $r=1$
. The model where all
$r=1$
. The model where all
![]() ${\lambda}_x$
are the same will be referred to as the homogeneous model; when
${\lambda}_x$
are the same will be referred to as the homogeneous model; when
![]() $r=1$
we will say that it is a short-range model.
$r=1$
we will say that it is a short-range model.
(ii) Continuous tree model on
 $\mathbb{R}_+$
$\mathbb{R}_+$
Suppose that ‘trees’ (or rather their centres) arrive on
![]() $\mathbb{R}_+$
as a Poisson process of rate 1. Namely, the number of trees that appeared on [0, x],
$\mathbb{R}_+$
as a Poisson process of rate 1. Namely, the number of trees that appeared on [0, x],
![]() $x>0$
by time
$x>0$
by time
![]() $t>0$
is given by a number of points of two-dimensional Poisson process in a rectangle
$t>0$
is given by a number of points of two-dimensional Poisson process in a rectangle
![]() $[0,x]\times [0,t]$
. Each tree is a closed interval (one-dimensional circle) of a fixed radius 1. See Figure 1. There is a constant source of fire attached to the origin, point 0. Whenever a tree covering the origin appears, it immediately burns down together with the whole connected component of trees (overlapping circles) containing point 0. For the continuous model, we can similarly define N(t) and
$[0,x]\times [0,t]$
. Each tree is a closed interval (one-dimensional circle) of a fixed radius 1. See Figure 1. There is a constant source of fire attached to the origin, point 0. Whenever a tree covering the origin appears, it immediately burns down together with the whole connected component of trees (overlapping circles) containing point 0. For the continuous model, we can similarly define N(t) and
![]() $N^{\color{ForestGreen}{\textbf{G}}}(t)$
, as we did for the model on
$N^{\color{ForestGreen}{\textbf{G}}}(t)$
, as we did for the model on
![]() $\mathbb{Z}_+$
.
$\mathbb{Z}_+$
.

Figure 1. Continuous tree model on
![]() $\mathbb{R}_+$
.
$\mathbb{R}_+$
.
Also, to avoid making the paper unnecessarily cumbersome, we restrict our attention to the homogeneous version of model (ii), even though one can think of a more general setup.
Definition 1. Let
![]() $\tau_x$
,
$\tau_x$
,
![]() $x\in \mathbb{R}_+$
, be the time when point x is burnt by fire for the first time in the forest fire model (either (i) or (ii)). Similarly, let
$x\in \mathbb{R}_+$
, be the time when point x is burnt by fire for the first time in the forest fire model (either (i) or (ii)). Similarly, let
![]() $\tau_x^{\color{ForestGreen}{\textbf{G}}}$
be the first time when x is reachable by the green process. More formally,
$\tau_x^{\color{ForestGreen}{\textbf{G}}}$
be the first time when x is reachable by the green process. More formally,
The following statement applies to both models (i) and (ii).
Proposition 1. Let
![]() $\tau_x$
and
$\tau_x$
and
![]() $\tau_x^{\color{ForestGreen}{\textbf{G}}}$
be as defined above. Then there is a coupling between the green process and the forest fire process such that the following hold.
$\tau_x^{\color{ForestGreen}{\textbf{G}}}$
be as defined above. Then there is a coupling between the green process and the forest fire process such that the following hold.
The original forest fire process is always behind or equal to the green process, i.e.
 $\tau_x\ge \tau_x^{\color{ForestGreen}{\textbf{G}}}$
for all
$\tau_x\ge \tau_x^{\color{ForestGreen}{\textbf{G}}}$
for all
 $\omega$
.
$\omega$
.Nevertheless, every time the fire process burns a point never burnt before, its ‘spread’ coincides with that of the green process (see Figure 2): namely, for almost all
 $\omega$
there is an infinite increasing sequence of times
$\omega$
there is an infinite increasing sequence of times
 $t_i\to\infty$
,
$t_i\to\infty$
,
 $i = 1, 2,\ldots,$
such that
$i = 1, 2,\ldots,$
such that
 $N(t_i)=N^{\color{ForestGreen}{\textbf{G}}}(t_i)$
.
$N(t_i)=N^{\color{ForestGreen}{\textbf{G}}}(t_i)$
.

Figure 2.
![]() $\tau_x$
for the forest fire and green processes.
$\tau_x$
for the forest fire and green processes.
Proof. The first part of the statement follows immediately from the construction of the two processes on the same probability space. To show the second part, introduce the increasing sequence of stopping times
![]() $\sigma_i$
and locations
$\sigma_i$
and locations
![]() $u_i$
such that
$u_i$
such that
![]() $\sigma_0=u_0=0$
;
$\sigma_0=u_0=0$
;
![]() $\sigma_i>\sigma_{i-1}$
is the first time the fire burns a point never burnt before, and
$\sigma_i>\sigma_{i-1}$
is the first time the fire burns a point never burnt before, and
![]() $u_i$
is the rightmost point burnt by the fire at time
$u_i$
is the rightmost point burnt by the fire at time
![]() $\sigma_i$
. It is not hard to see that all
$\sigma_i$
. It is not hard to see that all
![]() $\sigma_i<\infty$
and
$\sigma_i<\infty$
and
![]() $u_i<\infty $
a.s.
$u_i<\infty $
a.s.
Then, at times
![]() $\sigma_i$
, the forest fire process coincides with the ‘green’ process, since at the infinitesimal moment before that, all the vertices to the right of
$\sigma_i$
, the forest fire process coincides with the ‘green’ process, since at the infinitesimal moment before that, all the vertices to the right of
![]() $u_{i-1}$
are in the same state for both processes.
$u_{i-1}$
are in the same state for both processes.
3. Non-homogeneous and long-range processes
The main result of this section is the following theorem.
Theorem 1. Assume that the forest fire process is the one described by model (i) for some r,
![]() $c_1$
, and
$c_1$
, and
![]() $c_2$
. Fix any
$c_2$
. Fix any
![]() $\kappa>(\!\log 2)^{-1}=1.442695\ldots.$
Then, for all large enough x,
$\kappa>(\!\log 2)^{-1}=1.442695\ldots.$
Then, for all large enough x,
Observe that this result does not depend on values
![]() $c_1,c_2,r$
. The proof of the above statement will follow from Sections 3.2.2 and 3.3.
$c_1,c_2,r$
. The proof of the above statement will follow from Sections 3.2.2 and 3.3.
Remark 2. By comparing
![]() $\tau_{x+1}$
with
$\tau_{x+1}$
with
![]() $\tau_x$
, it is not difficult to see that
$\tau_x$
, it is not difficult to see that
and hence to get by induction that
![]() $\mathbb{E}\tau_x<\infty$
for all
$\mathbb{E}\tau_x<\infty$
for all
![]() $x\ge 1$
. See the proof of Theorem 1.
$x\ge 1$
. See the proof of Theorem 1.
Remark 3. Using Propositions 1 and 4 (or Propositions 1 and 2 in the homogeneous case), which come later in the paper, it is easy to obtain that there is a sufficiently small constant
![]() $C>0$
such that
$C>0$
such that
![]() $\mathbb{P}(\tau_x\ge C \log x)\ge \mathbb{P}(\tau_x^{\color{ForestGreen}{\textbf{G}}} \ge C \log x)\to 1$
as
$\mathbb{P}(\tau_x\ge C \log x)\ge \mathbb{P}(\tau_x^{\color{ForestGreen}{\textbf{G}}} \ge C \log x)\to 1$
as
![]() $x\to\infty$
, and hence
$x\to\infty$
, and hence
![]() $\tau_x$
must be at least of order
$\tau_x$
must be at least of order
![]() $\log x$
.
$\log x$
.
Remark 4. We conjecture that the correct power of the
![]() $\log$
in the statement of Theorem 1 should in fact be 1, as in [Reference Volkov10], thus matching the lower bound. See also Corollary 1.
$\log$
in the statement of Theorem 1 should in fact be 1, as in [Reference Volkov10], thus matching the lower bound. See also Corollary 1.
Recall that the ‘green process’ is the modified version of the forest fire process in which there are no fires at all, and that
![]() $N^{\color{ForestGreen}{\textbf{G}}}(t)$
is the size of the connected cluster of occupied vertices including the origin for the green process. We start with a special case.
$N^{\color{ForestGreen}{\textbf{G}}}(t)$
is the size of the connected cluster of occupied vertices including the origin for the green process. We start with a special case.
3.1. Short range non-homogeneous process
This is the special case of the process when
![]() $r=1$
, which we can study without reference to the green process, using Lemma 3 in [Reference van den Berg and Tóth4] about the invariance of the distribution of
$r=1$
, which we can study without reference to the green process, using Lemma 3 in [Reference van den Berg and Tóth4] about the invariance of the distribution of
![]() $\tau_x$
with respect to permutation of the rates
$\tau_x$
with respect to permutation of the rates
![]() $\lambda_1,\ldots,\lambda_x$
.
$\lambda_1,\ldots,\lambda_x$
.
It turns out that larger
![]() $\lambda$
correspond to smaller
$\lambda$
correspond to smaller
![]() $\tau_x$
, hence
$\tau_x$
, hence
![]() $\tau_x$
is stochastically bounded below and above by
$\tau_x$
is stochastically bounded below and above by
![]() $\tilde\tau_x/c_2$
and
$\tilde\tau_x/c_2$
and
![]() $\tilde\tau_x/c_1$
respectively, where
$\tilde\tau_x/c_1$
respectively, where
![]() $\tilde\tau_x$
is the distribution found in [Reference Volkov10]. In particular,
$\tilde\tau_x$
is the distribution found in [Reference Volkov10]. In particular,
![]() $\mathbb{E} \tau_x={\mathrm{O}}(\!\log x)$
.
$\mathbb{E} \tau_x={\mathrm{O}}(\!\log x)$
.
To see why this is true, note that by basic coupling, the fire process with rates
![]() $\lambda_1,\ldots, \lambda_{x-1}, c_2$
hits point x before
$\lambda_1,\ldots, \lambda_{x-1}, c_2$
hits point x before
![]() $\tau_x$
. Now the permutation invariance result of [Reference van den Berg and Tóth4, Lemma 3] states that the former has the same law as the hitting time of x by the fire process with rates
$\tau_x$
. Now the permutation invariance result of [Reference van den Berg and Tóth4, Lemma 3] states that the former has the same law as the hitting time of x by the fire process with rates
![]() $c_2, \lambda_1,\ldots, \lambda_{x-1}$
. Iterating the argument, we prove our claim.
$c_2, \lambda_1,\ldots, \lambda_{x-1}$
. Iterating the argument, we prove our claim.
Remark 5. It is straightforward that for the green process in this case we have
3.2. Long-range green process
Define
![]() $B_i=B_i(t)$
as the event that node i is vacant at time t. Then
$B_i=B_i(t)$
as the event that node i is vacant at time t. Then
![]() $B_i$
are independent and
$B_i$
are independent and
![]() $\mathbb{P}(B_i)={\mathrm{e}}^{-{\lambda}_i t}$
. Moreover,
$\mathbb{P}(B_i)={\mathrm{e}}^{-{\lambda}_i t}$
. Moreover,
that is, there is a vacant interval of length r somewhere on [0, n]. From equation (2) we have
 \begin{array}{*{20}{c}}{\mathbb{P}({N^{\color{ForestGreen}{\mathbf{G}}}}(t) < n) \le \sum\limits_{i = 0}^{n - r} \mathbb{P} (\bigcap\limits_{m = 1}^r {{B_{i + m}}} ) = \sum\limits_{i = 0}^{n - r} {{{\text{e}}^{ - ({\lambda _{i + 1}} + \ldots + {\lambda _{i + r}})t}}} = :{f_n}(t).} \hfill \\ \end{array}
\begin{array}{*{20}{c}}{\mathbb{P}({N^{\color{ForestGreen}{\mathbf{G}}}}(t) < n) \le \sum\limits_{i = 0}^{n - r} \mathbb{P} (\bigcap\limits_{m = 1}^r {{B_{i + m}}} ) = \sum\limits_{i = 0}^{n - r} {{{\text{e}}^{ - ({\lambda _{i + 1}} + \ldots + {\lambda _{i + r}})t}}} = :{f_n}(t).} \hfill \\ \end{array}
3.2.1. The homogeneous case
Without loss of generality assume that
![]() ${\lambda}_x={\lambda}=1$
. The next statement shows that the first time at which
${\lambda}_x={\lambda}=1$
. The next statement shows that the first time at which
![]() $N^{\color{ForestGreen}{\textbf{G}}}(t)\ge n$
is of order
$N^{\color{ForestGreen}{\textbf{G}}}(t)\ge n$
is of order
![]() $T\,:\!=\, {\log n}/r$
, where r is the range of the process.
$T\,:\!=\, {\log n}/r$
, where r is the range of the process.
Proposition 2. For every
![]() $\varepsilon>0$
we have
$\varepsilon>0$
we have
 \begin{align*}\mathbb{P}\bigl( N^{\color{ForestGreen}{\textbf{G}}}((1-\varepsilon)T)>n\bigr)&={\mathrm{o}}(1),\\ \mathbb{P}\bigl( N^{\color{ForestGreen}{\textbf{G}}}((1+\varepsilon)T)<n\bigr)&={\mathrm{o}}(1),\end{align*}
\begin{align*}\mathbb{P}\bigl( N^{\color{ForestGreen}{\textbf{G}}}((1-\varepsilon)T)>n\bigr)&={\mathrm{o}}(1),\\ \mathbb{P}\bigl( N^{\color{ForestGreen}{\textbf{G}}}((1+\varepsilon)T)<n\bigr)&={\mathrm{o}}(1),\end{align*}
as
![]() $n\to\infty$
.
$n\to\infty$
.
Let
![]() $p_n=p_n(t)\,:\!=\, \mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}(t)\ge n\bigr)$
, that is, the probability that on the set of vertices
$p_n=p_n(t)\,:\!=\, \mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}(t)\ge n\bigr)$
, that is, the probability that on the set of vertices
![]() $\{1,2\ldots,n\}$
there are no ‘holes’ of length of at least r, and site 0 is occupied. Observe that
$\{1,2\ldots,n\}$
there are no ‘holes’ of length of at least r, and site 0 is occupied. Observe that
![]() $p_n$
satisfies the following recursion:
$p_n$
satisfies the following recursion:
 \begin{align*}p_n&=\sum_{k=1}^{r} (1-\alpha) \alpha^{k-1} p_{n-k}, \quad n> r,\\p_1&=p_2=\cdots=p_{r-1}=1-{\mathrm{e}}^{-t},\end{align*}
\begin{align*}p_n&=\sum_{k=1}^{r} (1-\alpha) \alpha^{k-1} p_{n-k}, \quad n> r,\\p_1&=p_2=\cdots=p_{r-1}=1-{\mathrm{e}}^{-t},\end{align*}
where
![]() $\alpha=\alpha_t\,:\!=\, {\mathrm{e}}^{-t}$
. Indeed, in order to reach
$\alpha=\alpha_t\,:\!=\, {\mathrm{e}}^{-t}$
. Indeed, in order to reach
![]() $n>r$
, one must have an occupied vertex somewhere between 1 and r; the probability that the first such vertex is exactly at k is
$n>r$
, one must have an occupied vertex somewhere between 1 and r; the probability that the first such vertex is exactly at k is
and then we need to reach n from k. Therefore the asymptotic behaviour of
![]() $p_n$
will depend on the largest solution of the characteristic equation
$p_n$
will depend on the largest solution of the characteristic equation
 \begin{align}\xi^r- \sum_{k=0}^{r-1} (1-\alpha)\, \alpha^{(r-1)-k} \, \xi^{k}=0.\end{align}
\begin{align}\xi^r- \sum_{k=0}^{r-1} (1-\alpha)\, \alpha^{(r-1)-k} \, \xi^{k}=0.\end{align}
In particular, when
![]() $r=2$
we get
$r=2$
we get
![]() $ \xi_{1,2}={(1-\alpha\pm\sqrt{D})}/{2} $
, where
$ \xi_{1,2}={(1-\alpha\pm\sqrt{D})}/{2} $
, where
![]() $D=1+2\alpha-3\alpha^2$
, resulting in
$D=1+2\alpha-3\alpha^2$
, resulting in
where
![]() $n=1,2,\ldots.$
$n=1,2,\ldots.$
While we cannot solve (4) explicitly except for
![]() $r=2$
and
$r=2$
and
![]() $r=3$
, we can still find the critical value of t for a given n, i.e. T. Indeed, from (3) we have
$r=3$
, we can still find the critical value of t for a given n, i.e. T. Indeed, from (3) we have
and at the same time, since the unions of the events below are independent,
 \begin{align*}\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}(t)>n\bigr)&\le \mathbb{P}( (B_1^c\cup \cdots \cup B_r^c) \cap(B_{r+1}^c \dots B_{r+r}^c)\cap \cdots\cap (B_{Mr+1}^c\dots B_{Mr+r}^c))\\&=\prod_{k=0}^{M} \mathbb{P}((B_{kr+1} B_{kr+2} \dots B_{kr+r})^c)\\&= (1-{\mathrm{e}}^{-rt})^{\lfloor n/r\rfloor }\\&\le (1-{\mathrm{e}}^{-rt})^{ n/r-1 } ,\end{align*}
\begin{align*}\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}(t)>n\bigr)&\le \mathbb{P}( (B_1^c\cup \cdots \cup B_r^c) \cap(B_{r+1}^c \dots B_{r+r}^c)\cap \cdots\cap (B_{Mr+1}^c\dots B_{Mr+r}^c))\\&=\prod_{k=0}^{M} \mathbb{P}((B_{kr+1} B_{kr+2} \dots B_{kr+r})^c)\\&= (1-{\mathrm{e}}^{-rt})^{\lfloor n/r\rfloor }\\&\le (1-{\mathrm{e}}^{-rt})^{ n/r-1 } ,\end{align*}
where
![]() $M=\lfloor n/r \rfloor -1$
and
$M=\lfloor n/r \rfloor -1$
and
![]() $\lfloor x\rfloor$
denotes the integer part of
$\lfloor x\rfloor$
denotes the integer part of
![]() $x\in\mathbb{R}$
. Consequently
$x\in\mathbb{R}$
. Consequently
Thus Proposition 2 is proved.
3.2.2. The non-homogeneous case
Here we no longer assume that the
![]() ${\lambda}_x$
are the same for all x, as we did in Section 3.2.1.
${\lambda}_x$
are the same for all x, as we did in Section 3.2.1.
The following statement is trivial and its proof is thus omitted.
Proposition 3. The function
![]() $f_n(t)$
defined in (3) satisfies the following properties.
$f_n(t)$
defined in (3) satisfies the following properties.
For a fixed n,
 $f_n(t)$
is monotonically decreasing with range from
$f_n(t)$
is monotonically decreasing with range from
 $n-r+1$
to
$n-r+1$
to
 $0$
as t goes from
$0$
as t goes from
 $0$
to
$0$
to
 $+\infty$
.
$+\infty$
.For a fixed t,
 $f_n(t)$
is monotonically increasing in n and moreover
$f_n(t)$
is monotonically increasing in n and moreover
 $f_{n}(t)-f_{n-1}(t)\le {\mathrm{e}}^{-rc_1 t}$
.
$f_{n}(t)-f_{n-1}(t)\le {\mathrm{e}}^{-rc_1 t}$
.
Let us split the sum in
![]() $f_n(t)$
into r ‘almost’ equal parts according to the value of the remainder when i is divided by r. Namely, for
$f_n(t)$
into r ‘almost’ equal parts according to the value of the remainder when i is divided by r. Namely, for
![]() $j=0,1,\ldots,r-1$
let
$j=0,1,\ldots,r-1$
let
 \begin{equation*}f_{n,j}(t)=\sum_{k=0}^{\lfloor {(n-j-r)}/{r}\rfloor}{\mathrm{e}}^{-({\lambda}_{rk+j+1}+{\lambda}_{rk+j+2}+\dots+ {\lambda}_{rk+j+r})t} ,\end{equation*}
\begin{equation*}f_{n,j}(t)=\sum_{k=0}^{\lfloor {(n-j-r)}/{r}\rfloor}{\mathrm{e}}^{-({\lambda}_{rk+j+1}+{\lambda}_{rk+j+2}+\dots+ {\lambda}_{rk+j+r})t} ,\end{equation*}
and therefore
First we show that
Indeed, the upper bound follows from (3). To show the lower bound, note that at least one of
![]() $f_{n,j}(t)$
,
$f_{n,j}(t)$
,
![]() $j=0,1,\ldots,r-1$
, must be larger than
$j=0,1,\ldots,r-1$
, must be larger than
![]() $f_n(t)/r$
; without loss of generality, assume
$f_n(t)/r$
; without loss of generality, assume
![]() $f_{n,0}(t)\ge f_n(t)/r$
. Then we have
$f_{n,0}(t)\ge f_n(t)/r$
. Then we have
 \begin{align*}\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}(t) \ge n\bigr)&=\mathbb{P}\Biggl( \bigcap_{i=0}^{n-r} (B_{i+1}B_{i+2} \dots B_{i+r})^c \Biggr)\\&\le\mathbb{P}\Biggl( \bigcap_{k=0}^{\lfloor n/r \rfloor-1}(B_{rk+1} B_{rk+2}\dots B_{rk+r})^c\Biggr)\\&\stackrel{\text{indep.}}{\,=\,}\prod_{k=0}^{\lfloor n/r \rfloor-1}\mathbb{P} ( (B_{rk+1} B_{rk+2}\dots B_{rk+r})^c )\\&=\prod_{k=0}^{\lfloor n/r \rfloor-1}( 1-{\mathrm{e}}^{-({\lambda}_{rk+1}+\dots+{\lambda}_{rk+r})t} )\\&\le\exp\Biggl(-\sum_{k=0}^{\lfloor n/r \rfloor-1}{\mathrm{e}}^{-({\lambda}_{rk+1}+\dots+{\lambda}_{rk+r})t}\Biggr) \\&={\mathrm{e}}^{-f_{n,0}(t)}\\&\le {\mathrm{e}}^{-f_n(t)/r},\end{align*}
\begin{align*}\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}(t) \ge n\bigr)&=\mathbb{P}\Biggl( \bigcap_{i=0}^{n-r} (B_{i+1}B_{i+2} \dots B_{i+r})^c \Biggr)\\&\le\mathbb{P}\Biggl( \bigcap_{k=0}^{\lfloor n/r \rfloor-1}(B_{rk+1} B_{rk+2}\dots B_{rk+r})^c\Biggr)\\&\stackrel{\text{indep.}}{\,=\,}\prod_{k=0}^{\lfloor n/r \rfloor-1}\mathbb{P} ( (B_{rk+1} B_{rk+2}\dots B_{rk+r})^c )\\&=\prod_{k=0}^{\lfloor n/r \rfloor-1}( 1-{\mathrm{e}}^{-({\lambda}_{rk+1}+\dots+{\lambda}_{rk+r})t} )\\&\le\exp\Biggl(-\sum_{k=0}^{\lfloor n/r \rfloor-1}{\mathrm{e}}^{-({\lambda}_{rk+1}+\dots+{\lambda}_{rk+r})t}\Biggr) \\&={\mathrm{e}}^{-f_{n,0}(t)}\\&\le {\mathrm{e}}^{-f_n(t)/r},\end{align*}
hence
![]() $P\bigl(N^{\color{ForestGreen}{\textbf{G}}}(t)<n\bigr)\ge 1-{\mathrm{e}}^{-f_n(t)/r}$
.
$P\bigl(N^{\color{ForestGreen}{\textbf{G}}}(t)<n\bigr)\ge 1-{\mathrm{e}}^{-f_n(t)/r}$
.
Let
![]() $t_*=t_*(n,\alpha)$
be such that
$t_*=t_*(n,\alpha)$
be such that
![]() $f_n(t_*)=\alpha\in(0,1)$
; its existence and uniqueness follow from Proposition 3 and the fact that
$f_n(t_*)=\alpha\in(0,1)$
; its existence and uniqueness follow from Proposition 3 and the fact that
![]() $f_n({\cdot})$
is strictly decreasing on
$f_n({\cdot})$
is strictly decreasing on
![]() $[0,\infty)$
and continuous. Now set
$[0,\infty)$
and continuous. Now set
![]() $\alpha=1/2$
and define
$\alpha=1/2$
and define
![]() $\tilde T=t_*(n,1/2)$
; later we will establish that
$\tilde T=t_*(n,1/2)$
; later we will establish that
![]() $\tilde T={\mathrm{O}}(\!\log n)$
: see (5). Then
$\tilde T={\mathrm{O}}(\!\log n)$
: see (5). Then
Proposition 4. Fix a small
![]() $\varepsilon>0$
. Then, for any
$\varepsilon>0$
. Then, for any
![]() $c\in(0,c_1/c_2)$
and all large n,
$c\in(0,c_1/c_2)$
and all large n,
 \begin{align*}\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}(\tilde T-\varepsilon \tilde T\bigr)\ge n)&\le {\mathrm{e}}^{-n^{c\varepsilon}}, \\\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}(\tilde T+\varepsilon \tilde T\bigr)<n)&\le n^{-c\varepsilon}.\end{align*}
\begin{align*}\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}(\tilde T-\varepsilon \tilde T\bigr)\ge n)&\le {\mathrm{e}}^{-n^{c\varepsilon}}, \\\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}(\tilde T+\varepsilon \tilde T\bigr)<n)&\le n^{-c\varepsilon}.\end{align*}
Proof. Indeed, since
by summing up the left-hand side, the right-hand side, and
![]() $1/2$
of the above chain of inequalities, we immediately get
$1/2$
of the above chain of inequalities, we immediately get
Consequently
 \begin{equation*}f_n(\tilde T+\varepsilon \tilde T)=\sum_{i=0}^{n-r}\dfrac{{\mathrm{e}}^{-({\lambda}_{i+1}+\dots+{\lambda}_{i+r})\tilde T}}{{\mathrm{e}}^{({\lambda}_{i+1}+\dots+{\lambda}_{i+r})\varepsilon \tilde T}}\le\sum_{i=0}^{n-r} \dfrac{{\mathrm{e}}^{-({\lambda}_{i+1}+\dots+{\lambda}_{i+r})\tilde T}}{{\mathrm{e}}^{r\tilde T \cdot c_1 \varepsilon }}\le \dfrac{1}{2\, (2n-2r+2)^{ {c_1 \varepsilon }/{c_2} }}.\end{equation*}
\begin{equation*}f_n(\tilde T+\varepsilon \tilde T)=\sum_{i=0}^{n-r}\dfrac{{\mathrm{e}}^{-({\lambda}_{i+1}+\dots+{\lambda}_{i+r})\tilde T}}{{\mathrm{e}}^{({\lambda}_{i+1}+\dots+{\lambda}_{i+r})\varepsilon \tilde T}}\le\sum_{i=0}^{n-r} \dfrac{{\mathrm{e}}^{-({\lambda}_{i+1}+\dots+{\lambda}_{i+r})\tilde T}}{{\mathrm{e}}^{r\tilde T \cdot c_1 \varepsilon }}\le \dfrac{1}{2\, (2n-2r+2)^{ {c_1 \varepsilon }/{c_2} }}.\end{equation*}
By the same token,
 \begin{align*}f_n(\tilde T-\varepsilon \tilde T)&=\sum_{i=0}^{n-r} {\mathrm{e}}^{-({\lambda}_{i+1}+\dots+{\lambda}_{i+r})\tilde T}\times {\mathrm{e}}^{({\lambda}_{i+1}+\dots+{\lambda}_{i+r})\varepsilon \tilde T}\\&\ge \sum_{i=0}^{n-r} {\mathrm{e}}^{-({\lambda}_{i+1}+\dots+{\lambda}_{i+r})\tilde T}\times {\mathrm{e}}^{r\tilde T \cdot c_1 \varepsilon } \\&\ge \dfrac{1}{2}\, (2n-2r+2)^{ {c_1 \varepsilon }/{c_2} }.\end{align*}
\begin{align*}f_n(\tilde T-\varepsilon \tilde T)&=\sum_{i=0}^{n-r} {\mathrm{e}}^{-({\lambda}_{i+1}+\dots+{\lambda}_{i+r})\tilde T}\times {\mathrm{e}}^{({\lambda}_{i+1}+\dots+{\lambda}_{i+r})\varepsilon \tilde T}\\&\ge \sum_{i=0}^{n-r} {\mathrm{e}}^{-({\lambda}_{i+1}+\dots+{\lambda}_{i+r})\tilde T}\times {\mathrm{e}}^{r\tilde T \cdot c_1 \varepsilon } \\&\ge \dfrac{1}{2}\, (2n-2r+2)^{ {c_1 \varepsilon }/{c_2} }.\end{align*}
As a result,
and
which yields the statement of the theorem, since
![]() ${c_1\varepsilon}/{c_2}>c\varepsilon$
.
${c_1\varepsilon}/{c_2}>c\varepsilon$
.
Corollary 1. There exists
![]() $C_1>0$
such that
$C_1>0$
such that
Proof. From Proposition 4 we get that for some non-random
![]() $C_1>0$
$C_1>0$
By choosing a sequence
![]() $n_j=j^A$
,
$n_j=j^A$
,
![]() $j=1,2,\ldots$
for some large
$j=1,2,\ldots$
for some large
![]() $A>0$
such that
$A>0$
such that
![]() $Ac\varepsilon>1$
, by the Borel–Cantelli lemma a.s. for all large enough j, we have
$Ac\varepsilon>1$
, by the Borel–Cantelli lemma a.s. for all large enough j, we have
Using monotonicity of
![]() $\tau_x^{\color{ForestGreen}{\textbf{G}}}$
in x, and the fact that for each x there is a j such that
$\tau_x^{\color{ForestGreen}{\textbf{G}}}$
in x, and the fact that for each x there is a j such that
we conclude that
a.s. for all large x. As a result, by the second part of Proposition 1, which equivalently stated means that
![]() $\tau_x=\tau_x^{\color{ForestGreen}{\textbf{G}}}$
for infinitely many x, we obtain (6).
$\tau_x=\tau_x^{\color{ForestGreen}{\textbf{G}}}$
for infinitely many x, we obtain (6).
3.3. Coupling of the forest fire and green processes
Fix
![]() $\gamma\in (1,2)$
, and let us define the increasing sequence of times
$\gamma\in (1,2)$
, and let us define the increasing sequence of times
![]() $\gamma^k$
,
$\gamma^k$
,
![]() $k=1,2,\ldots.$
Let
$k=1,2,\ldots.$
Let
Proposition 5. Let
![]() $n_k$
and
$n_k$
and
![]() $T_k$
be as defined above. Then the following holds.
$T_k$
be as defined above. Then the following holds.
 $n_k=\exp\{r\, \tilde c_k\, \gamma^k\}$
for some
$n_k=\exp\{r\, \tilde c_k\, \gamma^k\}$
for some
 $\tilde c_k\in [c_1-{\mathrm{o}}(1),c_2+{\mathrm{o}}(1)]$
.
$\tilde c_k\in [c_1-{\mathrm{o}}(1),c_2+{\mathrm{o}}(1)]$
.Fix any positive
 $\delta$
. Then
$\delta$
. Then
 $\gamma^k\in[T_k-\delta, T_k]$
provided k is large enough.
$\gamma^k\in[T_k-\delta, T_k]$
provided k is large enough.
Proof. The first part of the statement follows immediately from the definition of f. To show the second part, note that from Proposition 3 we have
On the other hand, for any small positive
![]() $\delta$
,
$\delta$
,
so from Proposition 3 we have
 \begin{align*}f_{n_k-1}(T_k-\delta)&=f_{n_k}(T_k-\delta)- [f_{n_k}(T_k-\delta)-f_{n_k-1}(T_k-\delta)]\\& \ge\dfrac{{\mathrm{e}}^{r c_1 \delta} }{2} - {\mathrm{e}}^{-r c_1 (T_k-\delta)}\\&\ge \dfrac 12 +\dfrac{r c_1 \delta}{2} - {\mathrm{e}}^{-r c_1 (T_k-\delta)}.\end{align*}
\begin{align*}f_{n_k-1}(T_k-\delta)&=f_{n_k}(T_k-\delta)- [f_{n_k}(T_k-\delta)-f_{n_k-1}(T_k-\delta)]\\& \ge\dfrac{{\mathrm{e}}^{r c_1 \delta} }{2} - {\mathrm{e}}^{-r c_1 (T_k-\delta)}\\&\ge \dfrac 12 +\dfrac{r c_1 \delta}{2} - {\mathrm{e}}^{-r c_1 (T_k-\delta)}.\end{align*}
For k large enough,
![]() $\gamma^k$
is also large, and so is
$\gamma^k$
is also large, and so is
![]() $T_k\ge \gamma^k$
, which yields that
$T_k\ge \gamma^k$
, which yields that
![]() $ {\mathrm{e}}^{-r c_1 (T_k-\delta)}$
is very small, yielding that the right-hand side of the above expression is larger than
$ {\mathrm{e}}^{-r c_1 (T_k-\delta)}$
is very small, yielding that the right-hand side of the above expression is larger than
![]() $1/2$
, so
$1/2$
, so
by monotonicity of
![]() $f_{n_k-1}({\cdot})$
. Consequently
$f_{n_k-1}({\cdot})$
. Consequently
![]() $\gamma^k\in[T_k-\delta, T_k]$
for all large k.
$\gamma^k\in[T_k-\delta, T_k]$
for all large k.
Corollary 2. For any
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
 \begin{align}\begin{split}\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}( (1-\varepsilon)\, \gamma^k )\ge n_k\bigr)&\to 0,\\\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}( (1+\varepsilon)\, \gamma^k )< n_k\bigr)&\to 0,\end{split}\end{align}
\begin{align}\begin{split}\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}( (1-\varepsilon)\, \gamma^k )\ge n_k\bigr)&\to 0,\\\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}( (1+\varepsilon)\, \gamma^k )< n_k\bigr)&\to 0,\end{split}\end{align}
as
![]() $k\to\infty$
.
$k\to\infty$
.
Now we are ready to present the proof of our main result.
Proof of Theorem
Proof of Theorem 1.Fix
![]() $k\ge 1$
and define the new
$k\ge 1$
and define the new
![]() ${{\color{blue}{blue}}}$
process
${{\color{blue}{blue}}}$
process
![]() $S^{\color{blue}{\textbf{B}}}$
, which takes values in
$S^{\color{blue}{\textbf{B}}}$
, which takes values in
![]() $\{0,1\}^{\mathbb{Z}_+}$
, as follows. Let
$\{0,1\}^{\mathbb{Z}_+}$
, as follows. Let
![]() $\tau_{n_k}^{(1)}$
be the first time when the fire process reaches
$\tau_{n_k}^{(1)}$
be the first time when the fire process reaches
![]() $n_k$
. Up to this time
$n_k$
. Up to this time
![]() $S^{\color{blue}{\textbf{B}}}$
completely coincides with the fire process
$S^{\color{blue}{\textbf{B}}}$
completely coincides with the fire process
![]() $S^{\color{red}{\textbf{F}}}$
. However, at this hitting time, we set
$S^{\color{red}{\textbf{F}}}$
. However, at this hitting time, we set
![]() $S^{\color{blue}{\textbf{B}}}\bigl(x,\tau_{n_k}^{(1)}\bigr)=0$
for all x (not just those reachable from 0). After this, the blue process evolves again exactly like the fire process on the same probability space using the same collection of the Poisson process
$S^{\color{blue}{\textbf{B}}}\bigl(x,\tau_{n_k}^{(1)}\bigr)=0$
for all x (not just those reachable from 0). After this, the blue process evolves again exactly like the fire process on the same probability space using the same collection of the Poisson process
![]() ${\mathcal{P}}_x$
(see the beginning of the paper), until the next time when
${\mathcal{P}}_x$
(see the beginning of the paper), until the next time when
![]() $n_k$
is burnt, at which point the blue process restarts again with zeros everywhere. Thus
$n_k$
is burnt, at which point the blue process restarts again with zeros everywhere. Thus
![]() $S^{\color{blue}{\textbf{B}}}(x,t)$
is a renewal process with the renewal times
$S^{\color{blue}{\textbf{B}}}(x,t)$
is a renewal process with the renewal times
![]() $\tau_{n_k}^{(i)}$
,
$\tau_{n_k}^{(i)}$
,
![]() $i=1,2,\ldots,$
where
$i=1,2,\ldots,$
where
![]() $\tau_{n_k}^{(i)}$
are the consecutive times when the fire process reaches
$\tau_{n_k}^{(i)}$
are the consecutive times when the fire process reaches
![]() $n_k$
. Moreover, the blue process and the fire process are trivially coupled such that
$n_k$
. Moreover, the blue process and the fire process are trivially coupled such that
 \begin{alignat*}{3}S^{\color{blue}{\textbf{B}}}(x,t)&=S^{\color{red}{\textbf{F}}}(x,t)\quad&&\text{for $t<\tau_{n_k}^{(1)}$ and all}\, {\textit{x},}\\S^{\color{blue}{\textbf{B}}}(x,t)&=S^{\color{red}{\textbf{F}}}(x,t)\quad&&\text{for all}\, {\textit{t}}\, {\text {and}\, x\le n_k,}\\S^{\color{blue}{\textbf{B}}}(x,t)&\le S^{\color{red}{\textbf{F}}}(x,t)\quad&&\text{for all } {\textit{t}\,} {\text{and} \,x> n_k.}\end{alignat*}
\begin{alignat*}{3}S^{\color{blue}{\textbf{B}}}(x,t)&=S^{\color{red}{\textbf{F}}}(x,t)\quad&&\text{for $t<\tau_{n_k}^{(1)}$ and all}\, {\textit{x},}\\S^{\color{blue}{\textbf{B}}}(x,t)&=S^{\color{red}{\textbf{F}}}(x,t)\quad&&\text{for all}\, {\textit{t}}\, {\text {and}\, x\le n_k,}\\S^{\color{blue}{\textbf{B}}}(x,t)&\le S^{\color{red}{\textbf{F}}}(x,t)\quad&&\text{for all } {\textit{t}\,} {\text{and} \,x> n_k.}\end{alignat*}
Let
![]() $\rho_i$
(resp.
$\rho_i$
(resp.
![]() $\rho_i^{\color{red}{\textbf{F}}}$
),
$\rho_i^{\color{red}{\textbf{F}}}$
),
![]() $i=1,2,\ldots,$
be the rightmost point burnt by the blue process (resp. the fire process) at time
$i=1,2,\ldots,$
be the rightmost point burnt by the blue process (resp. the fire process) at time
![]() $\tau_{n_k}^{(i)}$
. Define the inter-arrival times
$\tau_{n_k}^{(i)}$
. Define the inter-arrival times
![]() $\Delta_{n_k}^{(i)}=\tau_{n_k}^{(i)}-\tau_{n_k}^{(i-1)}$
,
$\Delta_{n_k}^{(i)}=\tau_{n_k}^{(i)}-\tau_{n_k}^{(i-1)}$
,
![]() $i=2,3,\ldots,$
with the convention that
$i=2,3,\ldots,$
with the convention that
![]() $\Delta_{n_k}^{(1)}=\tau_{n_k}^{(1)}=\tau_{n_k}$
. From the definition of the blue process, it follows that the random variables
$\Delta_{n_k}^{(1)}=\tau_{n_k}^{(1)}=\tau_{n_k}$
. From the definition of the blue process, it follows that the random variables
![]() $\xi_i=\bigl(\Delta_{n_k}^{(i)},\rho_i\bigr)$
,
$\xi_i=\bigl(\Delta_{n_k}^{(i)},\rho_i\bigr)$
,
![]() $i=2,3,\ldots$
are i.i.d.
$i=2,3,\ldots$
are i.i.d.
By construction
![]() $\rho_1=\rho_1^{\color{red}{\textbf{F}}}$
, that is, the rightmost burnt point is the same for the fire and the blue processes when the fire process reaches
$\rho_1=\rho_1^{\color{red}{\textbf{F}}}$
, that is, the rightmost burnt point is the same for the fire and the blue processes when the fire process reaches
![]() $n_k$
for the first time; however, this does not necessarily hold for the times
$n_k$
for the first time; however, this does not necessarily hold for the times
![]() $\tau_{n_k}^{(i)}$
,
$\tau_{n_k}^{(i)}$
,
![]() $i\ge 2$
. At the same time we can claim the following.
$i\ge 2$
. At the same time we can claim the following.
Lemma 1. We have
 $\rho_i \le \rho_i^{\color{red}{\textbf{F}}}$
for all i,
$\rho_i \le \rho_i^{\color{red}{\textbf{F}}}$
for all i,on the event
 $\rho_i\le \rho_{i-1}$
we have
$\rho_i\le \rho_{i-1}$
we have
 $\rho_i^{\color{red}{\textbf{F}}}=\rho_i$
.
$\rho_i^{\color{red}{\textbf{F}}}=\rho_i$
.
Proof of lemma. The first part of the lemma trivially follows from the fact that
![]() $S^{\color{blue}{\textbf{B}}}(x,t)\le S^{\color{red}{\textbf{F}}}(x,t)$
for all x and t. To show the second statement, note that at time
$S^{\color{blue}{\textbf{B}}}(x,t)\le S^{\color{red}{\textbf{F}}}(x,t)$
for all x and t. To show the second statement, note that at time
![]() $s=\tau^{(i-1)}_{n_k}$
we have
$s=\tau^{(i-1)}_{n_k}$
we have
Until time
![]() $\tau_{n_k}^{(i)}$
, the fire and the blue processes coincide on
$\tau_{n_k}^{(i)}$
, the fire and the blue processes coincide on
![]() $[0,\rho_{i-1}]$
. Since
$[0,\rho_{i-1}]$
. Since
![]() $\rho_{i}\le \rho_{i-1}$
,
$\rho_{i}\le \rho_{i-1}$
,
where
![]() $S^{\color{blue}{\textbf{B}}}(x,t-0)$
denotes the state of x in the infinitesimal moment just before time t. However, since the blue and the fire process coincide on
$S^{\color{blue}{\textbf{B}}}(x,t-0)$
denotes the state of x in the infinitesimal moment just before time t. However, since the blue and the fire process coincide on
![]() $[0,\rho_{i-1}]$
, this also means that
$[0,\rho_{i-1}]$
, this also means that
and thus the fire cannot reach any point beyond
![]() $\rho_i$
.
$\rho_i$
.
Now fix an
![]() $\varepsilon>0$
so small that
$\varepsilon>0$
so small that
For each
![]() $j=1,2,\ldots,$
let
$j=1,2,\ldots,$
let
![]() $S^{\color{ForestGreen}{\textbf{G}}}_j$
denote a version of the green process which is reset everywhere to zero at time
$S^{\color{ForestGreen}{\textbf{G}}}_j$
denote a version of the green process which is reset everywhere to zero at time
![]() $\tau_{n_k}^{(j-1)}$
, i.e. we have
$\tau_{n_k}^{(j-1)}$
, i.e. we have
![]() $S^{\color{ForestGreen}{\textbf{G}}}_j\bigl(x,\tau_{n_k}^{(j-1)}\bigr)=0$
for all
$S^{\color{ForestGreen}{\textbf{G}}}_j\bigl(x,\tau_{n_k}^{(j-1)}\bigr)=0$
for all
![]() $x\in \mathbb{Z}_+$
, with the convention
$x\in \mathbb{Z}_+$
, with the convention
![]() $\tau_{n_k}^{(0)}\equiv 0$
; thus
$\tau_{n_k}^{(0)}\equiv 0$
; thus
![]() $S^{\color{ForestGreen}{\textbf{G}}}_j\equiv S^{\color{ForestGreen}{\textbf{G}}}_1$
. Define
$S^{\color{ForestGreen}{\textbf{G}}}_j\equiv S^{\color{ForestGreen}{\textbf{G}}}_1$
. Define
 \begin{align*}E_{k,j}=\bigl\{&\text{for the green process $S^{\color{ForestGreen}{\textbf{G}}}_j$ there exists a subinterval of } (0, n_{k+1}]\\&\text{of length}\, {\textit{r}}\, \text {that has no Poisson arrivals during the time }\bigl[0,\Delta_{n_k}^{(j)}+\Delta_{n_k}^{(j+1)}\bigr]\bigr\}\end{align*}
\begin{align*}E_{k,j}=\bigl\{&\text{for the green process $S^{\color{ForestGreen}{\textbf{G}}}_j$ there exists a subinterval of } (0, n_{k+1}]\\&\text{of length}\, {\textit{r}}\, \text {that has no Poisson arrivals during the time }\bigl[0,\Delta_{n_k}^{(j)}+\Delta_{n_k}^{(j+1)}\bigr]\bigr\}\end{align*}
as well as
![]() $\alpha_k= \mathbb{P}(E_{k,j})$
; note that this probability does not depend on j since
$\alpha_k= \mathbb{P}(E_{k,j})$
; note that this probability does not depend on j since
![]() $\Delta_{n_k}^{(j)}$
are i.i.d.
$\Delta_{n_k}^{(j)}$
are i.i.d.
Lemma 2. We have
![]() $\alpha_k\to 0$
as
$\alpha_k\to 0$
as
![]() $k\to\infty$
.
$k\to\infty$
.
Proof of lemma. Recall
![]() $\tau_x^{\color{ForestGreen}{\textbf{G}}}$
from Definition 1 and apply Corollary 2. We have shown that
$\tau_x^{\color{ForestGreen}{\textbf{G}}}$
from Definition 1 and apply Corollary 2. We have shown that
and
where
![]() ${\mathrm{o}}(1)\to 0$
as
${\mathrm{o}}(1)\to 0$
as
![]() $k\to\infty$
. From (8), (9), and (10) it follows that
$k\to\infty$
. From (8), (9), and (10) it follows that
 \begin{align*}\mathbb{P}(E_{k,j})& \le \mathbb{P}\bigl(E_{k,j} \cap \bigl\{\Delta_{n_k}^{(j)}+\Delta_{n_k}^{(j+1)}>2(1-\varepsilon)\gamma^k\bigr\}\bigr)+2\,\mathbb{P}(\tau_{n_k}<(1-\varepsilon)\gamma^k)\\ &\le\mathbb{P}\bigl(\tau_{n_{k+1}}^{\color{ForestGreen}{\textbf{G}}}> 2 (1-\varepsilon)\gamma^k\bigr)+{\mathrm{o}}(1)\le\mathbb{P}\bigl(\tau_{n_{k+1}}^{\color{ForestGreen}{\textbf{G}}}> \gamma (1+\varepsilon) \gamma^k \bigr)+{\mathrm{o}}(1)\\&=\mathbb{P}\bigl(\tau_{n_{k+1}}^{\color{ForestGreen}{\textbf{G}}}> (1+\varepsilon) \gamma^{k+1} \bigr)+{\mathrm{o}}(1)\le {\mathrm{o}}(1)+{\mathrm{o}}(1), \nonumber\end{align*}
\begin{align*}\mathbb{P}(E_{k,j})& \le \mathbb{P}\bigl(E_{k,j} \cap \bigl\{\Delta_{n_k}^{(j)}+\Delta_{n_k}^{(j+1)}>2(1-\varepsilon)\gamma^k\bigr\}\bigr)+2\,\mathbb{P}(\tau_{n_k}<(1-\varepsilon)\gamma^k)\\ &\le\mathbb{P}\bigl(\tau_{n_{k+1}}^{\color{ForestGreen}{\textbf{G}}}> 2 (1-\varepsilon)\gamma^k\bigr)+{\mathrm{o}}(1)\le\mathbb{P}\bigl(\tau_{n_{k+1}}^{\color{ForestGreen}{\textbf{G}}}> \gamma (1+\varepsilon) \gamma^k \bigr)+{\mathrm{o}}(1)\\&=\mathbb{P}\bigl(\tau_{n_{k+1}}^{\color{ForestGreen}{\textbf{G}}}> (1+\varepsilon) \gamma^{k+1} \bigr)+{\mathrm{o}}(1)\le {\mathrm{o}}(1)+{\mathrm{o}}(1), \nonumber\end{align*}
where
![]() ${\mathrm{o}}(1)\to 0$
as
${\mathrm{o}}(1)\to 0$
as
![]() $k\to\infty$
.
$k\to\infty$
.
Corollary 3. For
![]() $j=1,2,\ldots $
we have
$j=1,2,\ldots $
we have
Proof. The result follows from the construction of
![]() $S^{\color{ForestGreen}{\textbf{G}}}_j$
and
$S^{\color{ForestGreen}{\textbf{G}}}_j$
and
![]() $S^{\color{red}{\textbf{F}}}$
which are both functionals of the collection of the Poisson processes
$S^{\color{red}{\textbf{F}}}$
which are both functionals of the collection of the Poisson processes
![]() ${\mathcal{P}}_x$
,
${\mathcal{P}}_x$
,
![]() $x\in \mathbb{Z}_+$
; in particular,
$x\in \mathbb{Z}_+$
; in particular,
for
![]() $t\in\bigl[\tau_{n_k}^{(j)},\tau_{n_k}^{(j+1)}\bigr]$
and
$t\in\bigl[\tau_{n_k}^{(j)},\tau_{n_k}^{(j+1)}\bigr]$
and
![]() $x\in \bigl[\rho_j^{\color{red}{\textbf{F}}},n_{k+1}\bigr]$
.
$x\in \bigl[\rho_j^{\color{red}{\textbf{F}}},n_{k+1}\bigr]$
.
One of the fires that burns
![]() $n_k$
will eventually burn
$n_k$
will eventually burn
![]() $n_{k+1}$
as well, so we can write
$n_{k+1}$
as well, so we can write
where
 \begin{equation*}A_i=A_i^{(k)}=\bigcap_{j=1}^{i}\bigl\{\rho_j^{\color{red}{\textbf{F}}}<n_{k+1}\bigr\}\end{equation*}
\begin{equation*}A_i=A_i^{(k)}=\bigcap_{j=1}^{i}\bigl\{\rho_j^{\color{red}{\textbf{F}}}<n_{k+1}\bigr\}\end{equation*}
is a decreasing sequence of events. In other words,
![]() $A_i$
corresponds to the event that during the first i fires at point
$A_i$
corresponds to the event that during the first i fires at point
![]() $n_{k}$
, point
$n_{k}$
, point
![]() $n_{k+1}$
has not yet been burnt. Since
$n_{k+1}$
has not yet been burnt. Since
![]() $\Delta^{(i)}_{n_k}$
,
$\Delta^{(i)}_{n_k}$
,
![]() $i=1,2,\ldots,$
are i.i.d.,
$i=1,2,\ldots,$
are i.i.d.,
![]() $\Delta^{(1)}_{n_k}\equiv\tau_{n_k}$
, and
$\Delta^{(1)}_{n_k}\equiv\tau_{n_k}$
, and
![]() $\Delta^{(i+1)}_{n_k}$
is independent of
$\Delta^{(i+1)}_{n_k}$
is independent of
![]() $A_i$
for each i:
$A_i$
for each i:
 \begin{align}\mathbb{E} (\tau_{n_{k+1}})=\mathbb{E} \tau_{n_k}\cdot\Biggl[1+\sum_{i=1}^\infty \mathbb{P}(A_i)\Biggr].\end{align}
\begin{align}\mathbb{E} (\tau_{n_{k+1}})=\mathbb{E} \tau_{n_k}\cdot\Biggl[1+\sum_{i=1}^\infty \mathbb{P}(A_i)\Biggr].\end{align}
Our task now is to estimate
![]() $\mathbb{P}(A_i)$
where
$\mathbb{P}(A_i)$
where
![]() $i\ge 1$
. Let
$i\ge 1$
. Let
![]() $y=(y_0,y_1,\ldots,y_i)$
be a sequence of positive numbers of length
$y=(y_0,y_1,\ldots,y_i)$
be a sequence of positive numbers of length
![]() $i+1$
with the convention that
$i+1$
with the convention that
![]() $y_0\equiv+\infty$
. We say that
$y_0\equiv+\infty$
. We say that
![]() $y_j$
,
$y_j$
,
![]() $j=1,2,\ldots,i-1$
, is a weak local minimum if
$j=1,2,\ldots,i-1$
, is a weak local minimum if
For each such sequence y there exists a non-negative integer
![]() $\nu=\nu(y)\ge 0$
, which is a lower bound on the number of local minima, and the increasing sequence of indices
$\nu=\nu(y)\ge 0$
, which is a lower bound on the number of local minima, and the increasing sequence of indices
![]() $s(y)=(s_1(y),s_2(y),\ldots,s(y)_{\nu(y)})$
with the property
$s(y)=(s_1(y),s_2(y),\ldots,s(y)_{\nu(y)})$
with the property
 $s_1(y)=\inf\{j\ge 1\,:\, H_j(y)\text{ occurs}\}$
is the index of the first weak local minimum in the sequence y;
$s_1(y)=\inf\{j\ge 1\,:\, H_j(y)\text{ occurs}\}$
is the index of the first weak local minimum in the sequence y; $s_{m+1}(y)$
is the index of the first local minimum in the sequence y with index at least
$s_{m+1}(y)$
is the index of the first local minimum in the sequence y with index at least
 $s_m(y)+3$
;
$s_m(y)+3$
; $s_{\nu}(y)+3>i-1$
, or there is no local minimum with index greater than or equal to
$s_{\nu}(y)+3>i-1$
, or there is no local minimum with index greater than or equal to
 $s_{\nu}(y)+3$
.
$s_{\nu}(y)+3$
.
Set
![]() $\nu(y)=0$
if no weak local minima exist in y. (To illustrate this concept, consider the example where
$\nu(y)=0$
if no weak local minima exist in y. (To illustrate this concept, consider the example where
![]() $ y=(\infty,3,2,4,1,3,2,5)$
, then
$ y=(\infty,3,2,4,1,3,2,5)$
, then
![]() $\nu=2$
and
$\nu=2$
and
![]() $(s_1,s_2)=(2,6)$
. Note that the number of local minima here is
$(s_1,s_2)=(2,6)$
. Note that the number of local minima here is
![]() $3>\nu$
, since the middle local minimum is too close to the first one.)
$3>\nu$
, since the middle local minimum is too close to the first one.)
Now let
where
![]() $\rho_1,\rho_2,\ldots$
are defined at the beginning of the proof of the theorem, and observe that the second condition in the definition of
$\rho_1,\rho_2,\ldots$
are defined at the beginning of the proof of the theorem, and observe that the second condition in the definition of
![]() $s_m(y)$
ensures that
$s_m(y)$
ensures that
![]() $\sigma_{m+1}\ge \sigma_m+3$
, so the triples
$\sigma_{m+1}\ge \sigma_m+3$
, so the triples
![]() $(\sigma_m-1,\sigma_m,\sigma_m+1)$
are non-overlapping for distinct ms, implying, in turn, that the triples
$(\sigma_m-1,\sigma_m,\sigma_m+1)$
are non-overlapping for distinct ms, implying, in turn, that the triples
![]() $(\rho_{\sigma_m-1}$
,
$(\rho_{\sigma_m-1}$
,
![]() $\rho_{\sigma_m}$
,
$\rho_{\sigma_m}$
,
![]() $\rho_{\sigma_m+1})$
are independent for distinct ms. As a result,
$\rho_{\sigma_m+1})$
are independent for distinct ms. As a result,
due to the symmetry between
![]() $\rho_{\sigma_m+2},\rho_{\sigma_m+3},\rho_{\sigma_m+4}$
. Since the
$\rho_{\sigma_m+2},\rho_{\sigma_m+3},\rho_{\sigma_m+4}$
. Since the
![]() $\rho_i$
are i.i.d., we therefore conclude that
$\rho_i$
are i.i.d., we therefore conclude that
![]() $\nu(y)$
is stochastically larger than a
$\nu(y)$
is stochastically larger than a
![]() $\operatorname{Binomial}(\lfloor (i+1)/3\rfloor,1/3)$
random variable.
$\operatorname{Binomial}(\lfloor (i+1)/3\rfloor,1/3)$
random variable.
By Lemma 1
![]() $\rho_{j+1}^{\color{red}{\textbf{F}}}\ge \rho_{j+1}$
and moreover on the event
$\rho_{j+1}^{\color{red}{\textbf{F}}}\ge \rho_{j+1}$
and moreover on the event
![]() $H_j(\rho)$
, we have
$H_j(\rho)$
, we have
![]() $\rho_j^{\color{red}{\textbf{F}}}=\rho_j$
since
$\rho_j^{\color{red}{\textbf{F}}}=\rho_j$
since
![]() $\rho_{j}\le \rho_{j-1}$
. Since also
$\rho_{j}\le \rho_{j-1}$
. Since also
![]() $\bigl(\rho_{j}^{\color{red}{\textbf{F}}}=\bigr)\rho_{j}\le \rho_{j+1} \bigl(\le \rho^{\color{red}{\textbf{F}}}_{j+1}\bigr)$
on
$\bigl(\rho_{j}^{\color{red}{\textbf{F}}}=\bigr)\rho_{j}\le \rho_{j+1} \bigl(\le \rho^{\color{red}{\textbf{F}}}_{j+1}\bigr)$
on
![]() $H_j(\rho)$
, by Lemma 1 and Corollary 3,
$H_j(\rho)$
, by Lemma 1 and Corollary 3,
By the law of iterated expectations,
where
![]() $(\rho)_i\,:\!=\, ({+}\infty,\rho_1,\rho_2,\ldots,\rho_i)$
, and the supremum is taken over all sequences y of length
$(\rho)_i\,:\!=\, ({+}\infty,\rho_1,\rho_2,\ldots,\rho_i)$
, and the supremum is taken over all sequences y of length
![]() $i+1$
with
$i+1$
with
![]() $y_0=+\infty$
and all other elements being positive. However, when
$y_0=+\infty$
and all other elements being positive. However, when
![]() $\nu(y)=m$
, for any realization of
$\nu(y)=m$
, for any realization of
![]() $s(y)=(\sigma_1,\ldots,\sigma_m)$
we have
$s(y)=(\sigma_1,\ldots,\sigma_m)$
we have
 \begin{align}\mathbb{P}(A_i \,|\, (\rho)_i=y)&=\mathbb{P}\Biggl( \bigcap_{j=1}^i \bigl\{\rho_{i}^{\color{red}{\textbf{F}}} < n_{k+1}\bigr\} \,|\, (\rho)_i=y \Biggr) \nonumber \\ & \le\mathbb{P}\Biggl( \bigcap_{l=1}^m \bigl[\bigl\{\rho_{\sigma_l+1}^{\color{red}{\textbf{F}}} < n_{k+1}\bigr\}\cap H_{\sigma_l}(\rho)\bigr] \,|\,(\rho)_i=y \Biggr)\le \alpha_k^m\end{align}
\begin{align}\mathbb{P}(A_i \,|\, (\rho)_i=y)&=\mathbb{P}\Biggl( \bigcap_{j=1}^i \bigl\{\rho_{i}^{\color{red}{\textbf{F}}} < n_{k+1}\bigr\} \,|\, (\rho)_i=y \Biggr) \nonumber \\ & \le\mathbb{P}\Biggl( \bigcap_{l=1}^m \bigl[\bigl\{\rho_{\sigma_l+1}^{\color{red}{\textbf{F}}} < n_{k+1}\bigr\}\cap H_{\sigma_l}(\rho)\bigr] \,|\,(\rho)_i=y \Biggr)\le \alpha_k^m\end{align}
due to the independence of the triples
![]() $\{\rho_{l-1},\rho_l,\rho_{l+1}\}$
for different
$\{\rho_{l-1},\rho_l,\rho_{l+1}\}$
for different
![]() $l\in s(y)$
. Consequently
$l\in s(y)$
. Consequently
 \begin{align}\mathbb{P}(A_i)&=\mathbb{P}\Biggl(A_i \cap \Biggl(\bigcup_{m=0}^\infty\{\nu(y)=m\}\Biggr)\Biggr)\notag \\&=\sum_{m=0}^\infty \mathbb{P}(A_i,\nu(y) =m)\nonumber\\&\le \mathbb{P}(\nu(y)=0)+\sum_{m=1}^{\lfloor i/10\rfloor+1} \mathbb{P}(A_i,\nu(y)=m)+\sum_{m=\lfloor i/10\rfloor+2}^{\infty} \mathbb{P}(A_i,\nu(y)=m)\nonumber\\& \overset{ \text{by (12)} }{\le}\mathbb{P}(\nu(y)=0)+\alpha_k\,\mathbb{P}\biggl(1\le \nu(y)\le \dfrac{i}{10}+1\biggr) +\sum_{m=\lfloor i/10\rfloor+2}^{\infty} \alpha_k^m\nonumber\\&\le \mathbb{P}(\nu(y)=0)+ \alpha_k\,2 {\mathrm{e}}^{-c_4 i} +\dfrac{\alpha_k^{1+i/10}}{1-\alpha_k},\end{align}
\begin{align}\mathbb{P}(A_i)&=\mathbb{P}\Biggl(A_i \cap \Biggl(\bigcup_{m=0}^\infty\{\nu(y)=m\}\Biggr)\Biggr)\notag \\&=\sum_{m=0}^\infty \mathbb{P}(A_i,\nu(y) =m)\nonumber\\&\le \mathbb{P}(\nu(y)=0)+\sum_{m=1}^{\lfloor i/10\rfloor+1} \mathbb{P}(A_i,\nu(y)=m)+\sum_{m=\lfloor i/10\rfloor+2}^{\infty} \mathbb{P}(A_i,\nu(y)=m)\nonumber\\& \overset{ \text{by (12)} }{\le}\mathbb{P}(\nu(y)=0)+\alpha_k\,\mathbb{P}\biggl(1\le \nu(y)\le \dfrac{i}{10}+1\biggr) +\sum_{m=\lfloor i/10\rfloor+2}^{\infty} \alpha_k^m\nonumber\\&\le \mathbb{P}(\nu(y)=0)+ \alpha_k\,2 {\mathrm{e}}^{-c_4 i} +\dfrac{\alpha_k^{1+i/10}}{1-\alpha_k},\end{align}
since
for some
![]() $c_4>0$
, by the large deviation theory (see e.g. [Reference den Hollander7]). Finally, observe that on
$c_4>0$
, by the large deviation theory (see e.g. [Reference den Hollander7]). Finally, observe that on
![]() $i\ge 2$
$i\ge 2$
due to the symmetry of all permutations of
![]() $[1,2,\ldots,i]$
.
$[1,2,\ldots,i]$
.
Trivially
![]() $\mathbb{P}(A_1)\le 1$
, so by (13)
$\mathbb{P}(A_1)\le 1$
, so by (13)
 \begin{equation*}\sum_{i=1}^\infty \mathbb{P}(A_i)\le 1+\sum_{i=2}^\infty\biggl[\dfrac 1{i!}+\alpha_k\biggl(2 {\mathrm{e}}^{-c_4 i} +\dfrac{\alpha_k^{i/10}}{1-\alpha_k}\biggr) \biggr]=e-1+{\mathrm{o}}(1),\end{equation*}
\begin{equation*}\sum_{i=1}^\infty \mathbb{P}(A_i)\le 1+\sum_{i=2}^\infty\biggl[\dfrac 1{i!}+\alpha_k\biggl(2 {\mathrm{e}}^{-c_4 i} +\dfrac{\alpha_k^{i/10}}{1-\alpha_k}\biggr) \biggr]=e-1+{\mathrm{o}}(1),\end{equation*}
where
![]() ${\mathrm{o}}(1)\to 0$
as
${\mathrm{o}}(1)\to 0$
as
![]() $k\to\infty$
, since
$k\to\infty$
, since
![]() $\alpha_k\to 0$
. Therefore (11) gives
$\alpha_k\to 0$
. Therefore (11) gives
 \begin{align*} \mathbb{E} (\tau_{n_{k+1}})&=\mathbb{E} \tau_{n_k}\cdot\Biggl[1+\sum_{i=1}^\infty \mathbb{P}(A_i)\Biggr]\le(e+{\mathrm{o}}(1))\cdot \mathbb{E} \tau_{n_k},\end{align*}
\begin{align*} \mathbb{E} (\tau_{n_{k+1}})&=\mathbb{E} \tau_{n_k}\cdot\Biggl[1+\sum_{i=1}^\infty \mathbb{P}(A_i)\Biggr]\le(e+{\mathrm{o}}(1))\cdot \mathbb{E} \tau_{n_k},\end{align*}
yielding that for any fixed
![]() $\delta>0$
$\delta>0$
for all sufficiently large k.
For each
![]() $x>0$
one can find a unique k such that
$x>0$
one can find a unique k such that
![]() $n_{k-1}< x\le n_{k}$
, and by Proposition 5,
$n_{k-1}< x\le n_{k}$
, and by Proposition 5,
whence
where the power can be made arbitrarily close to
![]() $(\!\log 2)^{-1}=1.442695\dots $
by choosing
$(\!\log 2)^{-1}=1.442695\dots $
by choosing
![]() $\gamma\uparrow 2$
and
$\gamma\uparrow 2$
and
![]() $\delta\downarrow 0$
. This proves Theorem 1.
$\delta\downarrow 0$
. This proves Theorem 1.
4. Continuous tree model on
 $\mathbb{R}_+$
$\mathbb{R}_+$
We want to get some estimates for the ‘green’ process in the case of the continuous space model, i.e. the one where by time
![]() $t\ge 0$
we have a Poisson point process on
$t\ge 0$
we have a Poisson point process on
![]() $\mathbb{R}_+$
(the set of occupied sites) in space–time with intensity
$\mathbb{R}_+$
(the set of occupied sites) in space–time with intensity
![]() ${\mathrm{d}} x\otimes {\mathrm{d}} t$
, and each point is the centre of a circle of radius 1.
${\mathrm{d}} x\otimes {\mathrm{d}} t$
, and each point is the centre of a circle of radius 1.
We say that two sites x and y of the Poisson process are connected if
![]() $|x-y|\le 1$
. We assume that 0 is always occupied. With these definitions we can also define the cluster of occupied sites containing zero, which will be the subset of points of the Poisson process
$|x-y|\le 1$
. We assume that 0 is always occupied. With these definitions we can also define the cluster of occupied sites containing zero, which will be the subset of points of the Poisson process
![]() $x_1=x_1(t)$
,
$x_1=x_1(t)$
,
![]() $x_2=x_2(t)$
,
$x_2=x_2(t)$
,
![]() $\dots$
,
$\dots$
,
![]() $x_{n(t)}=x_{n(t)}(t)$
such that
$x_{n(t)}=x_{n(t)}(t)$
such that
where
![]() $n=n(t)$
is the number of sites in the cluster. Let
$n=n(t)$
is the number of sites in the cluster. Let
![]() $N^{\color{red}{\textbf{F}}}(t)=x_{n(t)}(t)$
be the location of the rightmost site in the cluster, and let
$N^{\color{red}{\textbf{F}}}(t)=x_{n(t)}(t)$
be the location of the rightmost site in the cluster, and let
![]() $\tau_x^{\color{red}{\textbf{F}}} $
,
$\tau_x^{\color{red}{\textbf{F}}} $
,
![]() $x>0$
, be the smallest positive time for which
$x>0$
, be the smallest positive time for which
![]() $x\le N^{\color{red}{\textbf{F}}}(t)$
; thus
$x\le N^{\color{red}{\textbf{F}}}(t)$
; thus
We will find the estimate for
![]() $N^{\color{ForestGreen}{\textbf{G}}}(t)$
and
$N^{\color{ForestGreen}{\textbf{G}}}(t)$
and
![]() $\tau_x^{\color{ForestGreen}{\textbf{G}}}$
. Similar results can be found in the literature; see e.g. Proposition 5.2 in [Reference Asmussen, Ivanovs and Rønn Nielsen1].
$\tau_x^{\color{ForestGreen}{\textbf{G}}}$
. Similar results can be found in the literature; see e.g. Proposition 5.2 in [Reference Asmussen, Ivanovs and Rønn Nielsen1].
Proposition 6. For the green process in the continuous model on
![]() $\mathbb{R}_+$
, we have
$\mathbb{R}_+$
, we have
 \begin{align*}\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}(\!\log x)\ge x\bigr)&={\mathrm{o}}(1),\\\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}(\!\log x +3\log \log x\bigr)\le x )&={\mathrm{o}}(1).\end{align*}
\begin{align*}\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}(\!\log x)\ge x\bigr)&={\mathrm{o}}(1),\\\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}(\!\log x +3\log \log x\bigr)\le x )&={\mathrm{o}}(1).\end{align*}
Proof. Let
![]() $W_1=x_1$
,
$W_1=x_1$
,
![]() $W_i=x_{i}-x_{i-1}$
,
$W_i=x_{i}-x_{i-1}$
,
![]() $i\ge 2$
. Then
$i\ge 2$
. Then
![]() $W_i$
are i.i.d. exponentially distributed random variables with rate t. We can compute the Laplace transform of
$W_i$
are i.i.d. exponentially distributed random variables with rate t. We can compute the Laplace transform of
![]() $N^{\color{ForestGreen}{\textbf{G}}}(t)$
as follows:
$N^{\color{ForestGreen}{\textbf{G}}}(t)$
as follows:
 \begin{align*} \mathbb{E} \bigl[ {\mathrm{e}}^{-{\lambda} N^{\color{ForestGreen}{\textbf{G}}}(t)} \bigr] &= \mathbb{E}\bigl[ {\mathrm{e}}^{-{\lambda} \sum_{i=1}^{n(t)} W_i} \bigr] \notag \\&= \sum_{m=0}^{\infty} \mathbb{E}\bigl[ {\mathrm{e}}^{-{\lambda} \sum_{i=1}^{m} W_i} {\textbf{1}}_{\{n(t)=m\}} \bigr] \nonumber\\ \nonumber&= \sum_{m=0}^{\infty} \mathbb{E}\Biggl[ \prod_{i=1}^m {\mathrm{e}}^{-{\lambda} W_i} {\textbf{1}}_{\{ W_i\leq 1\}}\times {\textbf{1}}_{\{ W_{m+1}> 1\}} \Biggr] \notag \\&= \sum_{m=0}^{\infty} \mathbb{E}\bigl[ {\mathrm{e}}^{-{\lambda} w_1} {\textbf{1}}_{\{ w_1\leq 1\}} \bigr]^m\times \mathbb{P}[ w_1>1] \notag\\&= \sum_{m=0}^{\infty} \biggl[ \dfrac{t}{t+{\lambda}} (1-{\mathrm{e}}^{-{\lambda}-t}) \biggr]^m \times {\mathrm{e}}^{-t} \notag \\&= \dfrac{({\lambda}+t){\mathrm{e}}^{-t}}{{\lambda}+t{\mathrm{e}}^{-{\lambda}-t}}.\end{align*}
\begin{align*} \mathbb{E} \bigl[ {\mathrm{e}}^{-{\lambda} N^{\color{ForestGreen}{\textbf{G}}}(t)} \bigr] &= \mathbb{E}\bigl[ {\mathrm{e}}^{-{\lambda} \sum_{i=1}^{n(t)} W_i} \bigr] \notag \\&= \sum_{m=0}^{\infty} \mathbb{E}\bigl[ {\mathrm{e}}^{-{\lambda} \sum_{i=1}^{m} W_i} {\textbf{1}}_{\{n(t)=m\}} \bigr] \nonumber\\ \nonumber&= \sum_{m=0}^{\infty} \mathbb{E}\Biggl[ \prod_{i=1}^m {\mathrm{e}}^{-{\lambda} W_i} {\textbf{1}}_{\{ W_i\leq 1\}}\times {\textbf{1}}_{\{ W_{m+1}> 1\}} \Biggr] \notag \\&= \sum_{m=0}^{\infty} \mathbb{E}\bigl[ {\mathrm{e}}^{-{\lambda} w_1} {\textbf{1}}_{\{ w_1\leq 1\}} \bigr]^m\times \mathbb{P}[ w_1>1] \notag\\&= \sum_{m=0}^{\infty} \biggl[ \dfrac{t}{t+{\lambda}} (1-{\mathrm{e}}^{-{\lambda}-t}) \biggr]^m \times {\mathrm{e}}^{-t} \notag \\&= \dfrac{({\lambda}+t){\mathrm{e}}^{-t}}{{\lambda}+t{\mathrm{e}}^{-{\lambda}-t}}.\end{align*}
Using the Taylor expansion at
![]() ${\lambda} =0$
, we get the first moments of
${\lambda} =0$
, we get the first moments of
![]() $N^{\color{ForestGreen}{\textbf{G}}}(t)$
:
$N^{\color{ForestGreen}{\textbf{G}}}(t)$
:
It is easy to check that
for
![]() $\operatorname{Re} {\lambda}>-1$
, so
$\operatorname{Re} {\lambda}>-1$
, so
Consequently, as
![]() $t\to\infty$
,
$t\to\infty$
,
 \begin{align*}\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}(t)>{\mathrm{e}}^t\bigr)&=\mathbb{P}\bigl(t{\mathrm{e}}^{-t} N^{\color{ForestGreen}{\textbf{G}}}(t) >t\bigr)={\mathrm{o}}(1),\\\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}(t)<{\mathrm{e}}^t/t^2\bigr)&=\mathbb{P}\bigl(t{\mathrm{e}}^{-t} N^{\color{ForestGreen}{\textbf{G}}}(t) <1/t\bigr)={\mathrm{o}}(1).\end{align*}
\begin{align*}\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}(t)>{\mathrm{e}}^t\bigr)&=\mathbb{P}\bigl(t{\mathrm{e}}^{-t} N^{\color{ForestGreen}{\textbf{G}}}(t) >t\bigr)={\mathrm{o}}(1),\\\mathbb{P}\bigl(N^{\color{ForestGreen}{\textbf{G}}}(t)<{\mathrm{e}}^t/t^2\bigr)&=\mathbb{P}\bigl(t{\mathrm{e}}^{-t} N^{\color{ForestGreen}{\textbf{G}}}(t) <1/t\bigr)={\mathrm{o}}(1).\end{align*}
This in turn implies
and
which converges to zero, implying the statement of the proposition.
The following statement can be proved following verbatim the lines of the proof in Section 3.3 with
![]() $x_k=\gamma^k$
, since the estimate (7) is ensured by Proposition 6.
$x_k=\gamma^k$
, since the estimate (7) is ensured by Proposition 6.
Theorem 2. For the continuous model of forest fires on
![]() $\mathbb{R}_+$
, for any
$\mathbb{R}_+$
, for any
![]() $\delta>0$
,
$\delta>0$
,
for all x large enough.
Acknowledgements
In memory of Francis Comets 1956–2022.
M.M. and S.V. would like to acknowledge the hospitality of University Paris-Diderot; F.C. wished to acknowledge the hospitality of Lund University. We are extremely grateful and obliged to the anonymous referees who provided very detailed and useful remarks which allowed us to greatly improve the quality of this paper.
Funding information
S.V.’s research is partially supported by Swedish Science Foundation grants VR 2014–5157 and VR 2019-04173, and Crafoord foundation grant 20190667.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.