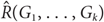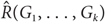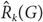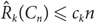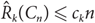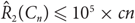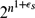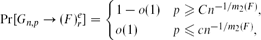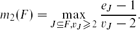For given graphs G1,…, Gk, the size-Ramsey number 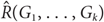 $\hat R({G_1}, \ldots ,{G_k})$
is the smallest integer m for which there exists a graph H on m edges such that in every k-edge colouring of H with colours 1,…,k, H contains a monochromatic copy of Gi of colour i for some 1 ≤ i ≤ k. We denote
$\hat R({G_1}, \ldots ,{G_k})$
is the smallest integer m for which there exists a graph H on m edges such that in every k-edge colouring of H with colours 1,…,k, H contains a monochromatic copy of Gi of colour i for some 1 ≤ i ≤ k. We denote 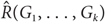 $\hat R({G_1}, \ldots ,{G_k})$
by
$\hat R({G_1}, \ldots ,{G_k})$
by 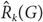 ${\hat R_k}(G)$
when G1 = ⋯ = Gk = G.
${\hat R_k}(G)$
when G1 = ⋯ = Gk = G.
Haxell, Kohayakawa and Łuczak showed that the size-Ramsey number of a cycle Cn is linear in n, 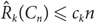 ${\hat R_k}({C_n}) \le {c_k}n$
for some constant ck. Their proof, however, is based on Szemerédi’s regularity lemma so no specific constant ck is known.
${\hat R_k}({C_n}) \le {c_k}n$
for some constant ck. Their proof, however, is based on Szemerédi’s regularity lemma so no specific constant ck is known.
In this paper, we give various upper bounds for the size-Ramsey numbers of cycles. We provide an alternative proof of 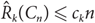 ${\hat R_k}({C_n}) \le {c_k}n$
, avoiding use of the regularity lemma, where ck is exponential and doubly exponential in k, when n is even and odd, respectively. In particular, we show that for sufficiently large n we have
${\hat R_k}({C_n}) \le {c_k}n$
, avoiding use of the regularity lemma, where ck is exponential and doubly exponential in k, when n is even and odd, respectively. In particular, we show that for sufficiently large n we have 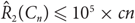 ${\hat R_2}({C_n}) \le {10^5} \times cn$
, where c = 6.5 if n is even and c = 1989 otherwise.
${\hat R_2}({C_n}) \le {10^5} \times cn$
, where c = 6.5 if n is even and c = 1989 otherwise.