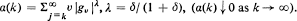Let {(Jn, Xn), n ≧ 0} be the standard J–X process of Markov renewal theory. Suppose {Jn, n ≧ 0} is irreducible, aperiodic and positive recurrent. It is shown using the strong mixing condition, that if 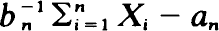 converges in distribution, where an, bn > 0 (bn → ∞) are real constants, then the limit law F must be stable. Suppose Q(x) = {PijHi(x)} is the semi-Markov matrix of {(JnXn), n ≧ 0}. Then the n-fold convolution, Q∗n(bnx + anbn), converges in distribution to F(x)Π if and only if
converges in distribution, where an, bn > 0 (bn → ∞) are real constants, then the limit law F must be stable. Suppose Q(x) = {PijHi(x)} is the semi-Markov matrix of {(JnXn), n ≧ 0}. Then the n-fold convolution, Q∗n(bnx + anbn), converges in distribution to F(x)Π if and only if 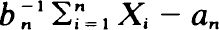 converges in distribution to F. Π is the matrix of stationary transition probabilities of {Jn, n ≧ 0}. Sufficient conditions on the Hi's are given for the convergence of the sequence of semi-Markov matrices to F(x)Π, where F is stable.
converges in distribution to F. Π is the matrix of stationary transition probabilities of {Jn, n ≧ 0}. Sufficient conditions on the Hi's are given for the convergence of the sequence of semi-Markov matrices to F(x)Π, where F is stable.

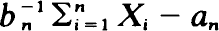 converges in distribution, where
converges in distribution, where 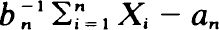 converges in distribution to
converges in distribution to 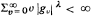 where
where 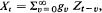 , where the identity is to be understood in the sense of convergence in distribution. Then {
, where the identity is to be understood in the sense of convergence in distribution. Then {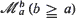 is the
is the 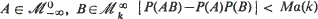 where
where