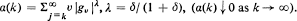Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
MATSUMOTO, Tadahiko
and
ARIYOSHI, Michiyasu
1975.
Nishi Nihon Hifuka,
Vol. 37,
Issue. 2,
p.
258.
Chanda, Kamal C.
1976.
Some comments on sample quantiles for dependent observations.
Communications in Statistics - Theory and Methods,
Vol. 5,
Issue. 14,
p.
1385.
Gorodetskii, V. V.
1978.
On the Strong Mixing Property for Linear Sequences.
Theory of Probability & Its Applications,
Vol. 22,
Issue. 2,
p.
411.
Chanda, Kamal C.
and
Kulp, Richard W.
1978.
On some nonparametric estimators for the linear markov scheme.
Communications in Statistics - Theory and Methods,
Vol. 7,
Issue. 5,
p.
427.
1980.
Statistical Inference for Stochastic Processes.
p.
415.
Withers, C. S.
1981.
Conditions for linear processes to be strong-mixing.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 57,
Issue. 4,
p.
477.
Chanda, Kamal C.
1981.
Statistical Distributions in Scientific Work.
p.
35.
Andrews, Donald W. K.
1984.
Non-strong mixing autoregressive processes.
Journal of Applied Probability,
Vol. 21,
Issue. 4,
p.
930.
Andrews, Donald W. K.
1985.
A Zero-One Result for the Least Squares Estimator.
Econometric Theory,
Vol. 1,
Issue. 1,
p.
85.
Pham, Tuan D.
and
Tran, Lanh T.
1985.
Some mixing properties of time series models.
Stochastic Processes and their Applications,
Vol. 19,
Issue. 2,
p.
297.
Athreya, Krishna B.
and
Pantula, Sastry G.
1986.
Mixing properties of harris chains and autoregressive processes.
Journal of Applied Probability,
Vol. 23,
Issue. 04,
p.
880.
Athreya, Krishna B.
and
Pantula, Sastry G.
1986.
A note on strong mixing of ARMA processes.
Statistics & Probability Letters,
Vol. 4,
Issue. 4,
p.
187.
Athreya, Krishna B.
and
Pantula, Sastry G.
1986.
Mixing properties of harris chains and autoregressive processes.
Journal of Applied Probability,
Vol. 23,
Issue. 4,
p.
880.
Roussas, George G.
and
Ioannides, D.
1987.
Moment inequalities for mixing sequences of random variables.
Stochastic Analysis and Applications,
Vol. 5,
Issue. 1,
p.
60.
Tran, L.T.
1989.
Recursive density estimation under dependence.
IEEE Transactions on Information Theory,
Vol. 35,
Issue. 5,
p.
1103.
Chanda, K. C.
and
Ruymgaart, F. H.
1990.
GENERAL LINEAR PROCESSES:A PROPERTY OF THE EMPIRICAL PROCESS APPLIED TO DENSITY AND MODE ESTIMATION.
Journal of Time Series Analysis,
Vol. 11,
Issue. 3,
p.
185.
Pötscher, Benedikt M.
and
Prucha, Ingmar R.
1991.
Basic structure of the asymptotic theory in dynamic nonlineaerco nometric models, part i: consistency and approximation concepts.
Econometric Reviews,
Vol. 10,
Issue. 2,
p.
125.
Härdle, Wolfgang
and
Vieu, Philippe
1992.
KERNEL REGRESSION SMOOTHING OF TIME SERIES.
Journal of Time Series Analysis,
Vol. 13,
Issue. 3,
p.
209.
F de Lima, Pedro J.
1996.
Nuisance parameter free properties of correlation integral based statistics.
Econometric Reviews,
Vol. 15,
Issue. 3,
p.
237.
Ho, Hwai-Chung
and
Hsing, Tailen
1997.
Limit theorems for functionals of moving averages.
The Annals of Probability,
Vol. 25,
Issue. 4,
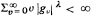 where λ = δ(1 + δ)−1. Define
where λ = δ(1 + δ)−1. Define 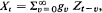 , where the identity is to be understood in the sense of convergence in distribution. Then {Xt; t = 0, ± 1, ···} is a strongly mixing stationary process in the sense that if
, where the identity is to be understood in the sense of convergence in distribution. Then {Xt; t = 0, ± 1, ···} is a strongly mixing stationary process in the sense that if 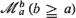 is the σ-fìeld generated by the random variables (r.v.) Xa, ···, Xb then for any
is the σ-fìeld generated by the random variables (r.v.) Xa, ···, Xb then for any 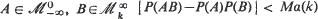 where M is a finite positive constant which depends only on ϕ0 and
where M is a finite positive constant which depends only on ϕ0 and