In this paper, we study the principal spectral theory of age-structured models with random diffusion. First, we provide an equivalent characteristic for the principal eigenvalue, the strong maximum principle and a positive strict super-solution. Then, we use the result to investigate the effects of diffusion rate on the principal eigenvalue. Finally, we study how the principal eigenvalue affects the global dynamics of the KPP model and verify that the principal eigenvalue being zero is a critical value.

In this article we consider the ergodic risk-sensitive control problem for a large class of multidimensional controlled diffusions on the whole space. We study the minimization and maximization problems under either a blanket stability hypothesis, or a near-monotone assumption on the running cost. We establish the convergence of the policy improvement algorithm for these models. We also present a more general result concerning the region of attraction of the equilibrium of the algorithm.

We discuss the zero-controllability and the zero-stabilizability for the nonnegative solutions to some Fisher-like models with nonlocal terms describing the dynamics of biological populations with diffusion, logistic term and migration. A necessary and sufficient condition for the nonnegative zero-stabilizabiity for a linear integro-partial differential equation is obtained in terms of the sign of the principal eigenvalue to a certain non-selfadjoint operator. For a related semilinear problem a necessary condition and a sufficient condition for the local nonnegative zero-stabilizability are also derived in terms of the magnitude of the above mentioned principal eigenvalue. The rate of stabilization corresponding to a simple feedback stabilizing control is dictated by the principal eigenvalue. A large principal eigenvalue leads to a fast stabilization to zero. A necessary condition and a sufficient condition for the stabilization to zero of the predator population in a predator-prey system is also investigated. Finally, a method to approximate the above mentioned principal eigenvalues is indicated.

We prove the existence of a principal eigenvalue associated to the∞-Laplacian plus lower order terms and the Neumann boundarycondition in a bounded smooth domain. As an application we getuniqueness and existence results for the Neumann problem and adecay estimate for viscosity solutions of the Neumann evolutionproblem.

In this paper we investigate the existence of positive solutions for nonlinear elliptic problems driven by the $p$-Laplacian with a nonsmooth potential (hemivariational inequality). Under asymptotic conditions that make the Euler functional indefinite and incorporate in our framework the asymptotically linear problems, using a variational approach based on nonsmooth critical point theory, we obtain positive smooth solutions. Our analysis also leads naturally to multiplicity results.

We give a criterion for extinction or local extinction of branching symmetric α-stable processes in terms of the principal eigenvalue for time-changed processes of symmetric α-stable processes. Here the branching rate and the branching mechanism are spatially dependent. In particular, the branching rate is allowed to be singular with respect to the Lebesgue measure. We apply this criterion to some branching processes.

We show that each point of the principal eigencurve of the nonlinear problem

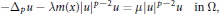$$-{{\Delta }_{p}}u-\text{ }\lambda m(x){{\left| u \right|}^{p-2}}u=\mu {{\left| u \right|}^{p-2}}u\,\,\text{in}\Omega ,$$

is stable (continuous) with respect to the exponent 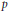$p$ varying in 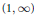$\left( 1,\infty \right)$; we also prove some convergence results of the principal eigenfunctions corresponding.