Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
  1. Home
  2. Search

Refine search

Refine search

Access:
Content type:
Publication date:
Apply   From and To filters
Subject: Show more
Journals Show more
Publishers: Show more
Societies Show more
Series: Show more
Collections: Show more

Actions for selected content:

Select all | Deselect all
  • View selected items
  • Export citations
  • Download PDF (zip)
  • Save to Kindle
  • Save to Dropbox
  • Save to Google Drive

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Please provide a title, maximum of 40 characters.
Cancel
×

2 results

  • 2 - Elliptic functions

  • from Part I - Modular forms and their variants
  • Eric D'Hoker, University of California, Los Angeles, Justin Kaidi, Kyushu University
  • Book:
    Modular Forms and String Theory
    Published online:
    28 November 2024
    Print publication:
    12 December 2024, pp 9-42

  • Summary

    Elliptic functions are introduced via the method of images following a review of periodic functions, Poisson summation, the unfolding trick, and analytic continuation applied to the Riemann zeta-function. The differential equations and addition formulas obeyed by periodic and elliptic functions are deduced from their Kronecker–Eisenstein series representation. The classic constructions of elliptic functions, in terms of their zeros and poles, are presented in terms of the Weierstrass elliptic function, the Jacobi elliptic functions, and the Jacobi theta-functions. The elliptic function theory developed here is placed in the framework of elliptic curves, Abelian differentials, and Abelian integrals.

  • Summability of alternating gap series

  • J. P. Keating, J. B. Reade
  • Journal:
    Proceedings of the Edinburgh Mathematical Society / Volume 43 / Issue 1 / February 2000
    Published online by Cambridge University Press:
    20 January 2009, pp. 95-101
    • Article
      • You have access
    • PDF
    • Export citation

  • The Abel and Cesàro summabilities of two alternating gap series are investigated. We prove that the series 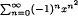is summable at x = 1 (in both senses), but that 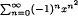is not. In 1907, Hardy obtained essentially the same result for the latter series; our proof is shorter and more elementary: we use the Poisson summation formula to derive an explicit estimate for the size of the oscillations as x → 1_. This represents an example of a general method for determining the Abel summability of similar series.