We demonstrate high efficiency second harmonic generation (SHG) of near infrared femtosecond pulses using a $\text{BiB}_{3}\text{O}_{6}$ crystal in a single-pass tight focusing geometry setup. A frequency doubling efficiency of $63\%$ is achieved, which is, to the best of our knowledge, the highest value ever reported in the femtosecond regime for such low energy (nJ-level) pumping pulses. Theoretical analyses of the pumping scheme focusing waist and the SHG efficiency are performed, by numerically solving the three wave mixing coupled equations in the plane-wave scenario and by running simulations with a commercial full 3D code. Simulations show a good agreement with the experimental data regarding both the efficiency and the pulse spectral profile. The simulated SHG pulse temporal profile presents the characteristic features of the group velocity mismatch broadening in a ‘thick’ crystal.

We consider a stationary moving average process with random coefficients, 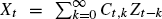, generated by an array, {Ct,k, t ∈ Z, k ≥ 0}, of random variables and a heavy-tailed sequence, {Zt, t ∈ Z}. We analyze the limit behavior using a point process analysis. As applications of our results we compare the limiting behavior of the moving average process with random coefficients with that of a standard MA(∞) process.