We investigate the stability properties of Muth's model of price movements when agents choose a production level using replicator dynamic learning. It turns out that when there is a discrete set of possible production levels, possible stable states and stability conditions differ between adaptive learning and replicator dynamic learning.

In the setting ofa real Hilbert space ${\cal H}$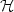, we investigate the asymptotic behavior, as time t goes to infinity, of trajectories of second-order evolutionequations

          ü(t) + γ$\dot{u}$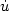(t) + ∇ϕ(u(t)) + A(u(t)) = 0,

where ∇ϕ is the gradient operator of a convexdifferentiable potential function ϕ : ${\cal H}\to \R$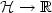, A : ${\cal H}\to {\cal H}$ is a maximal monotone operator which is assumed to beλ-cocoercive, and γ > 0 is a damping parameter.Potential and non-potential effects are associated respectively to∇ϕ and A. Under condition λγ2 > 1, it is proved that each trajectory asymptotically weaklyconverges to a zero of ∇ϕ + A. This condition, whichonly involves the non-potential operator and the dampingparameter, is sharp and consistent with time rescaling. Passingfrom weak to strong convergence of the trajectories is obtained byintroducing an asymptotically vanishing Tikhonov-like regularizingterm. As special cases, we recover the asymptotic analysis of theheavy ball with friction dynamic attached to a convex potential, thesecond-order gradient-projection dynamic, and the second-orderdynamic governed by the Yosida approximation of a general maximalmonotone operator. The breadth and flexibility of the proposed framework is illustrated through applications in the areas of constrained optimization,dynamical approach to Nash equilibria for noncooperative games, and asymptotic stabilization in the case of a continuum of equilibria.

In an uncongested transportation network, adding routes and capacity to an existing network must decrease, or at worst not change, the average time individuals require to travel through the network from a source to a destination. Braess (1968) discovered that the same is not true in congested networks. Here we give an example of a queuing network in which added capacity leads to an increase in the mean transit time for everyone. Self-seeking individuals are unable to refrain from using the additional capacity, even though using it leads to deterioration in the mean transit time. This example appears to be the first queuing network to demonstrate the general principle that in non-co-operative games with smooth payoff functions, user-determined equilibria generically deviate from system-optimal equilibria.

We consider the extension of optimal stopping problems to non-zero-sum strategic settings called stopping games. By imposing a monotone structure on the pay-offs of the game we establish the existence of a Nash equilibrium in non-randomized stopping times. As a corollary, we identify a class of games for which there are Nash equilibria in myopic stopping times. These games satisfy the strategic equivalent of the classical ‘monotone case' assumptions of the optimal stopping problem.