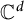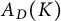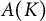In Gauthier, Manolaki, and Nestoridis (2021, Advances in Mathematics 381, 107649), in order to correct a false Mergelyan-type statement given in Gamelin and Garnett (1969, Transactions of the American Mathematical Society 143, 187–200) on uniform approximation on compact sets K in
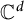 $\mathbb C^d$
, the authors introduced a natural function algebra
$\mathbb C^d$
, the authors introduced a natural function algebra
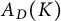 $A_D(K)$
which is smaller than the classical one
$A_D(K)$
which is smaller than the classical one
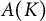 $A(K)$
. In the present paper, we investigate when these two algebras coincide and compare them with the classes of all plausibly approximable functions by polynomials or rational functions or functions holomorphic on open sets containing the compact set K. Finally, we introduce a notion of O-hull of K and strengthen known results.
$A(K)$
. In the present paper, we investigate when these two algebras coincide and compare them with the classes of all plausibly approximable functions by polynomials or rational functions or functions holomorphic on open sets containing the compact set K. Finally, we introduce a notion of O-hull of K and strengthen known results.