We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let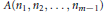 
$A({{n}_{1}},\,{{n}_{2}},\ldots ,\,{{n}_{m}}-1)$ be the normalized Fourier coefficients of a Maass cusp form on 
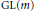$\text{GM(}m\text{)}$. In this paper, we study the cancellation of 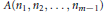$A({{n}_{1}},\,{{n}_{2}},\ldots ,\,{{n}_{m}}-1)$ over Beatty sequences.
