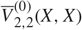In Weil (2001) formulae were proved for stationary Boolean models Z in ℝd with convex or polyconvex grains, which express the densities (specific mean values) of mixed volumes of Z in terms of related mean values of the underlying Poisson particle process X. These formulae were then used to show that in dimensions 2 and 3 the densities of mixed volumes of Z determine the intensity γ of X. For d = 4, a corresponding result was also stated, but the proof given was incomplete, since in the formula for the density of the Euler characteristic V̅0(Z) of Z a term $\overline V^{(0)}_{2,2}(X,X)$ was missing. This was pointed out in Goodey and Weil (2002), where it was also explained that a new decomposition result for mixed volumes and mixed translative functionals would be needed to complete the proof. Such a general decomposition result has recently been proved by Hug, Rataj, and Weil (2013), (2018) and is based on flag measures of the convex bodies involved. Here, we show that such flag representations not only lead to a correct derivation of the four-dimensional result, but even yield a corresponding uniqueness theorem in all dimensions. In the proof of the latter we make use of Alesker’s representation theorem for translation invariant valuations. We also discuss which shape information can be obtained in this way and comment on the situation in the nonstationary case.

We prove that the monodromy group of a reduced irreducible square system of general polynomial equations equals the symmetric group. This is a natural first step towards the Galois theory of general systems of polynomial equations, because arbitrary systems split into reduced irreducible ones upon monomial changes of variables. In particular, our result proves the multivariate version of the Abel–Ruffini theorem: the classification of general systems of equations solvable by radicals reduces to the classification of lattice polytopes of mixed volume 4 (which we prove to be finite in every dimension). We also notice that the monodromy of every general system of equations is either symmetric or imprimitive. The proof is based on a new result of independent importance regarding dual defectiveness of systems of equations: the discriminant of a reduced irreducible square system of general polynomial equations is a hypersurface unless the system is linear up to a monomial change of variables.

Nous présentons une expression explicite pour la hauteur normalisée d’une variété torique projective définie sur $\overline{\mathbb{Q}}$. Cette expression se décompose comme somme de contributions locales, chaque terme étant l’intégrale d’une certaine fonction concave et affine par morceaux, définie sur le polytope $Q_{\mathcal{A}}$ classiquement associé à l’action du tore. Plus généralement, nous obtenons une expression explicite pour la multihauteur normalisée d’un tore relative à plusieurs plongements monomiaux.

L’ensemble de fonctions introduit se comporte comme un analogue arithmétique du polytope $Q_{\mathcal{A}}$. En plus des formules pour les hauteur et multihauteurs, nous montrons que cet objet se comporte de manière naturelle par rapport à plusieurs constructions standard : décomposition en orbites, formation de joints, produits de Segre et plongements de Veronese.

La démonstration suit une démarche indirecte : à la place de la définition de la hauteur normalisée, on s’appuie sur le calcul d’une fonction de Hilbert arithmétique appropriée.

We present an explicit expression for the normalized height of a projective toric variety defined over $\overline{\mathbb{Q}}$. This expression decomposes as a sum of local contributions, each term being the integral of a certain function, concave and piecewise linear-affine, defined on the polytope $Q_{\mathcal{A}}$ classically associated with the torus action. More generally, we obtain an explicit expression for the normalized multiheight of a torus with respect to several monomial embeddings.

The set of functions introduced behaves as an arithmetic analogue of the polytope $Q_{\mathcal{A}}$. Besides the formulae for the height and multiheight, we show that this object behaves in a natural way with respect to several standard constructions: decomposition into orbits, joins, Segre products and Veronese embeddings.

The proof follows an indirect path: instead of the definition of the normalized height, we rely on the computation of an appropriate arithmetic Hilbert function.

A simple direct proof is given of Minkowski's result that the mean length of the orthogonal projection of a convex set in E3 onto an isotropic random line is (2π)–1 times the integral of mean curvature over its surface. This proof is generalised to a correspondingly direct derivation of an analogous formula for the mean projection of a convex set in En onto an isotropic random s-dimensional subspace in En. (The standard derivation of this, and a companion formula, to be found in Bonnesen and Fenchel's classic book on convex sets, is most indirect.) Finally, an alternative short inductive derivation (due to Matheron) of both formulae, by way of Steiner's formula, is presented.