We analyze domination properties and factorization of operators in Banach spaces through subspaces of 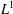 $L^{1}$-spaces. Using vector measure integration and extending classical arguments based on scalar integral bounds, we provide characterizations of operators factoring through subspaces of
$L^{1}$-spaces. Using vector measure integration and extending classical arguments based on scalar integral bounds, we provide characterizations of operators factoring through subspaces of 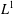 $L^{1}$-spaces of finite measures. Some special cases involving positivity and compactness of the operators are considered.
$L^{1}$-spaces of finite measures. Some special cases involving positivity and compactness of the operators are considered.
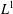 $L^{1}$-SPACES
$L^{1}$-SPACES