1 results
Kudla–Rapoport conjecture for Krämer models
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 29 June 2023, pp. 1673-1740
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
In this paper, we propose a modified Kudla–Rapoport conjecture for the Krämer model of unitary Rapoport–Zink space at a ramified prime, which is a precise identity relating intersection numbers of special cycles to derivatives of Hermitian local density polynomials. We also introduce the notion of special difference cycles, which has surprisingly simple description. Combining this with induction formulas of Hermitian local density polynomials, we prove the modified Kudla–Rapoport conjecture when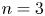
$n=3$. Our conjecture, combining with known results at inert and infinite primes, implies the arithmetic Siegel–Weil formula for all non-singular coefficients when the level structure of the corresponding unitary Shimura variety is defined by a self-dual lattice.
