Let $G$ be a geometrically finite
Kleinian group with parabolic elements and let $p$ be any parabolic fixed point of $G$. For each positive real
$\tau$, let ${\cal W}_{p}(\tau)$ denote the set of limit points of $G$ for which the inequality $$ | x-g(p) |
\leq |g^\prime(0)|^{\tau}$$ is satisfied for infinitely many elements $g$ in $G$. This subset of the limit set
is precisely the analogue of the set of $\tau$-well approximable numbers in the classical theory of metric
Diophantine approximation. In this paper we consider the following question. What is the `size' of the set
${\cal W}_{p}(\tau)$ expressed in terms of its Hausdorff dimension? We provide a complete answer, namely that
for $\tau \geq 1$,$$ \dim {\cal W}_{p} (\tau) = \min \left\{ \frac{\delta + \mbox{rk}(p) (\tau - 1) }{2
\tau - 1}, \, \frac{\delta}{\tau}\right\},$$ where $\mbox{rk}(p)$ denotes the rank of the parabolic fixed point
$p$.
1991 Mathematics Subject Classification: 11K55, 11K60, 11F99, 58D20.

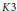
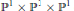
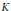
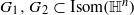 with the same set of axes are commensurable. We give some partial solutions.
with the same set of axes are commensurable. We give some partial solutions.