1 results
Parabolic category O, perverse sheaves on Grassmannians, Springer fibres and Khovanov homology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 954-992
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation
-
For a fixed parabolic subalgebra 𝔭 of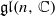
we prove that the centre of the principal block 𝒪0𝔭 of the parabolic category 𝒪 is naturally isomorphic to the cohomology ring H*(ℬ𝔭) of the corresponding Springer fibre. We give a diagrammatic description of 𝒪0𝔭 for maximal parabolic 𝔭 and give an explicit isomorphism to Braden’s description of the category PervB(G(k,n)) of Schubert-constructible perverse sheaves on Grassmannians. As a consequence Khovanov’s algebra ℋn is realised as the endomorphism ring of some object from PervB(G(n,n)) which corresponds under localisation and the Riemann–Hilbert correspondence to a full projective–injective module in the corresponding category 𝒪0𝔭. From there one can deduce that Khovanov’s tangle invariants are obtained from the more general functorial invariants in [C. Stroppel, Categorification of the Temperley Lieb category, tangles, and cobordisms via projective functors, Duke Math. J. 126(3) (2005), 547–596] by restriction.
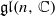we prove that the centre of the principal block 𝒪