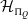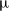We introduce and study a fermionisation procedure for the cohomological Hall algebra
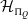 $\mathcal{H}_{\Pi_Q}$
of representations of a preprojective algebra, that selectively switches the cohomological parity of the BPS Lie algebra from even to odd. We do so by determining the cohomological Donaldson–Thomas invariants of central extensions of preprojective algebras studied in the work of Etingof and Rains, via deformed dimensional reduction. Via the same techniques, we determine the Borel–Moore homology of the stack of representations of the
$\mathcal{H}_{\Pi_Q}$
of representations of a preprojective algebra, that selectively switches the cohomological parity of the BPS Lie algebra from even to odd. We do so by determining the cohomological Donaldson–Thomas invariants of central extensions of preprojective algebras studied in the work of Etingof and Rains, via deformed dimensional reduction. Via the same techniques, we determine the Borel–Moore homology of the stack of representations of the
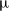 $\unicode{x03BC}$
-deformed preprojective algebra introduced by Crawley–Boevey and Holland, for all dimension vectors. This provides a common generalisation of the results of Crawley-Boevey and Van den Bergh on the cohomology of smooth moduli schemes of representations of deformed preprojective algebras and my earlier results on the Borel–Moore homology of the stack of representations of the undeformed preprojective algebra.
$\unicode{x03BC}$
-deformed preprojective algebra introduced by Crawley–Boevey and Holland, for all dimension vectors. This provides a common generalisation of the results of Crawley-Boevey and Van den Bergh on the cohomology of smooth moduli schemes of representations of deformed preprojective algebras and my earlier results on the Borel–Moore homology of the stack of representations of the undeformed preprojective algebra.