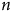Herein is exposed a simplified analytic proof of formulas for the characteristic functions of ordered partial sums of mutually independent identically distributed random variables. This problem which we had raised and solved in 1952 by another method, has since been treated by several authors (see Wendel [6]), and recently by de Smit [4], who made use of a kind of Wiener-Hopf decomposition†. On the contrary our present as well as our previous proof essentially uses the explicit solution of a certain singular integral equation in a complex domain.