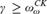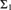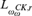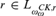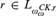1 results
OPTIMAL RESULTS ON RECOGNIZABILITY FOR INFINITE TIME REGISTER MACHINES
-
- Journal:
- The Journal of Symbolic Logic / Volume 80 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 22 December 2015, pp. 1116-1130
- Print publication:
- December 2015
-
- Article
- Export citation
-
Exploring further the properties of ITRM-recognizable reals started in [1], we provide a detailed analysis of recognizable reals and their distribution in Gödels constructible universe L. In particular, we show that new unrecognizable reals are generated at every index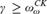
$\gamma \, \ge \,\omega _\omega ^{CK}$. We give a machine-independent characterization of recognizability by proving that a real r is recognizable if and only if it is 
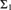${\Sigma _1}$-definable over 
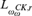${L_{\omega _\omega ^{CK,\,r}}}$ and that 
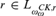$r\, \in \,{L_{\omega _\omega ^{CK,\,r}}}$ for every recognizable real r and show that either every or no r with 
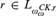$r\, \in \,{L_{\omega _\omega ^{CK,\,r}}}$ generated over an index stage 
${L_\gamma }$ is recognizable. Finally, the techniques developed along the way allow us to prove that the halting number for ITRMs is recognizable and that the set of ITRM-computable reals is not ITRM-decidable.
