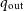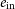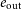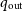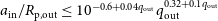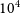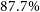Archimedes, the founder of statics and hydrostatics, in his mathematics and physics studies, created methods related to his inventions of new machines, for example, the method of mechanical theorems based on his lever invention. He also used the principles of decomposition and replication underlying his heat ray invention, and these two principles permeate his work. Analysis of Archimedes’ work shows how he was perhaps the first to use methodically a strategy for solving diverse complex problems. In this article, we use the term Archimedes Code to encompass the way Archimedes approached problems including those two principles. Archimedes was perhaps the first design theorist and the first to think systematically about how to address design challenges. Furthermore, his work demonstrates the fundamental role of engineering practice in advancing science. The new insights regarding the Archimedes Code and its value in design practice may inspire both design researchers and practitioners.

The three-body problem is famously chaotic, with no closed-form analytical solutions. However, hierarchical systems of three or more bodies can be stable over indefinite timescales. A system is considered hierarchical if the bodies can be divided into separate two-body orbits with distinct time and length scales, such that one orbit is only mildly affected by the gravitation of the other bodies. Previous work has mapped the stability of such systems at varying resolutions over a limited range of parameters, and attempts have been made to derive analytic and semi-analytic stability boundary fits to explain the observed phenomena. Certain regimes are understood relatively well. However, there are large regions of the parameter space which remain unmapped, and for which the stability boundary is poorly understood. We present a comprehensive numerical study of the stability boundary of hierarchical triples over a range of initial parameters. 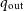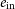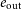Specifically, we consider the mass ratio of the inner binary to the outer third body ( $q_\mathrm{out}$ ), mutual inclination (i), initial mean anomaly and eccentricity of both the inner and outer binaries ( $e_\mathrm{in}$ and $e_\mathrm{out}$ respectively). We fit the dependence of the stability boundary on 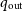$q_\mathrm{ out}$ as a threshold on the ratio of the inner binary’s semi-major axis to the outer binary’s pericentre separation 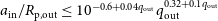$a_\mathrm{in}/R_\mathrm{p, out} \leq 10^{-0.6 + 0.04q_\mathrm{out}}q_\mathrm{out}^{0.32+0.1q_\mathrm{out}}$ for coplanar prograde systems. We develop an additional factor to account for mutual inclination. The resulting fit predicts the stability of 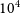$10^4$ orbits randomly initialised close to the stability boundary with 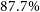$87.7\%$ accuracy.

The aim of this short paper is to examine the morphological categories of direction and direct-inverse marking in Northwestern Rma/Qiang (< Trans-Himalayan/Sino-Tibetan). Based on evidence from published sources (LaPolla and Huang 2003; H. Sūn 1981; Liú 1998, 1999; Sun and Evans 2013), it is argued that the verbal systems of some northern varieties are more characteristic of hierarchical alignment than previously recognized.