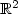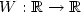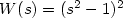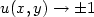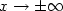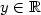We consider a class ofsemilinear elliptic equations of the form 15.7cm - $\varepsilon^{2}\Delta u(x,y)+a(x)W'(u(x,y))=0,\quad (x,y)\in{\mathbb{R}}^{2}$ 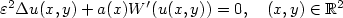 where $\varepsilon>0$
where $\varepsilon>0$ 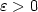 , $a:{\mathbb{R}}\to{\mathbb{R}}$
, $a:{\mathbb{R}}\to{\mathbb{R}}$ 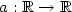 is a periodic, positive function and $W:{\mathbb{R}}\to{\mathbb{R}}$
is a periodic, positive function and $W:{\mathbb{R}}\to{\mathbb{R}}$ 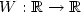 is modeled on the classical two well Ginzburg-Landaupotential $W(s)=(s^{2}-1)^{2}$
is modeled on the classical two well Ginzburg-Landaupotential $W(s)=(s^{2}-1)^{2}$ 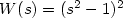 . We look for solutions to ([see full textsee full text])which verify theasymptotic conditions $u(x,y)\to\pm 1$
. We look for solutions to ([see full textsee full text])which verify theasymptotic conditions $u(x,y)\to\pm 1$ 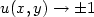 as $x\to\pm\infty$
as $x\to\pm\infty$ 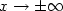 uniformly with respect to $y\in{\mathbb{R}}$
uniformly with respect to $y\in{\mathbb{R}}$ 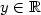 .We show via variationalmethods that if ε is sufficiently small and a is not constant, then ([see full textsee full text])admits infinitely many of such solutions, distinct up to translations, which do not exhibit one dimensional symmetries.
.We show via variationalmethods that if ε is sufficiently small and a is not constant, then ([see full textsee full text])admits infinitely many of such solutions, distinct up to translations, which do not exhibit one dimensional symmetries.
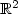 for a class of Allen-Cahn equations
for a class of Allen-Cahn equations