1 results
On random rotations
-
- Journal:
- Advances in Applied Probability / Volume 16 / Issue 3 / September 1984
- Published online by Cambridge University Press:
- 01 July 2016, pp. 638-655
- Print publication:
- September 1984
-
- Article
- Export citation
-
A body receives a sequence of rotations through a fixed angle about an axis whose direction is arbitrary. The probability distribution governing the resulting orientation of the body is determined. The problem is generalized to the case where the axis of each individual rotation makes the same angle, Θ, with an axis fixed in the body but is otherwise random. The resulting distribution is shown, in the case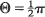
, to reduce to the Roberts-Ursell distribution for random walk on a sphere. Some diffusion limits are examined.
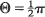, to reduce to the Roberts-Ursell distribution for random walk on a sphere. Some diffusion limits are examined.