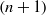1 results
Glicci ideals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 9 / September 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 1583-1591
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
-
A central problem in liaison theory is to decide whether every arithmetically Cohen–Macaulay subscheme of projective
$n$-space can be linked by a finite number of arithmetically Gorenstein schemes to a complete intersection. We show that this can indeed be achieved if the given scheme is also generically Gorenstein and we allow the links to take place in an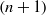 
$(n+ 1)$-dimensional projective space. For example, this result applies to all reduced arithmetically Cohen–Macaulay subschemes. We also show that every union of fat points in projective 3-space can be linked in the same space to a union of simple points in finitely many steps, and hence to a complete intersection in projective 4-space.
