Dialogues are turn-taking games which model debates about the satisfaction of logical formulas. A novel variant played over first-order structures gives rise to a notion of first-order satisfaction. We study the induced notion of validity for classical and intuitionistic first-order logic in the constructive setting of the calculus of inductive constructions. We prove that such material dialogue semantics for classical first-order logic admits constructive soundness and completeness proofs, setting it apart from standard model-theoretic semantics of first-order logic. Furthermore, we prove that completeness with regard to intuitionistic material dialogues fails in both constructive and classical settings. As an alternative, we propose material dialogues played over Kripke structures. These Kripke material dialogues exhibit constructive completeness when restricting to the negative fragment. The results concerning classical material dialogues have been mechanized using the Coq interactive theorem prover.

This work presents game semantics of Martin-Löf type theory (MLTT) equipped with the One, the Zero, the N, Pi, Sigma and Id types. Game semantics interprets a wide range of logic and computation, even the polymorphic 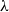$\lambda$-calculus; however, it has remained a well-known challenge in the past 25 years to achieve game semantics of dependent type theories such as MLTT, and past attempts lack directness or generality. For instance, the approach taken by Abramsky et al. interprets Sigma types indirectly by formal lists, not by games, making an interpretation of universes hopeless, and it is limited to a very specific class of dependent types. The difficulty of this challenge comes from a conflict between the extensionality of dependent types and the intensionality of game semantics. We overcome the challenge by inventing a novel variant of games, while we keep strategies unchanged, in such a way that this variant inherits the strong points of conventional game semantics. Also, our method enables an interpretation of subtyping on dependent types for the first time as game semantics. We finally give a new, game-semantic proof of the independence of Markov’s principle from MLTT. This proof illustrates an advantage of our intensional model over extensional ones such as Hyland’s effective topos.

The present work achieves a mathematical, in particular syntax-independent, formulation of dynamics and intensionality of computation in terms of games and strategies. Specifically, we give game semantics of a higher-order programming language that distinguishes programmes with the same value yet different algorithms (or intensionality) and the hiding operation on strategies that precisely corresponds to the (small-step) operational semantics (or dynamics) of the language. Categorically, our games and strategies give rise to a cartesian closed bicategory, and our game semantics forms an instance of a bicategorical generalisation of the standard interpretation of functional programming languages in cartesian closed categories. This work is intended to be a step towards a mathematical foundation of intensional and dynamic aspects of logic and computation; it should be applicable to a wide range of logics and computations.

We describe a sequent calculus μLJ with primitives for inductive andcoinductive datatypes and equip it with reduction rules allowing a sound translation ofGödel’s system T. We introduce the notion of a μ-closedcategory, relying on a uniform interpretation of open μLJformulas as strong functors. We show that any μ-closed category is asound model for μLJ. We then turn to the construction of a concreteμ-closed category based on Hyland-Ong game semantics. The model relieson three main ingredients: the construction of a general class of strong functors calledopen functors acting on the category of games and strategies, thesolution of recursive arena equations by exploiting cycles in arenas, andthe adaptation of the winning conditions of parity games to build initial algebras andterminal coalgebras for many open functors. We also prove a weak completeness result forthis model, yielding a normalisation proof for μLJ.

The paper gives a soundness and completeness proof for the implicative fragment of intuitionistic calculus with respect to the semantics of computability logic, which understands intuitionistic implication as interactive algorithmic reduction. This concept — more precisely, the associated concept of reducibility — is a generalization of Turing reducibility from the traditional, input/output sorts of problems to computational tasks of arbitrary degrees of interactivity.