1 results
Fast deterministic pricing of optionson Lévy driven assets
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 15 February 2004, pp. 37-71
- Print publication:
- January 2004
-
- Article
- Export citation
-
Arbitrage-free prices u of European contracts on risky assets whoselog-returns are modelled by Lévy processes satisfya parabolic partial integro-differential equation (PIDE) $\partial_t u + {\mathcal{A}}[u] = 0$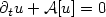
.This PIDE is localized tobounded domains and the error due to this localization isestimated. The localized PIDE is discretized by theθ-scheme in time and a wavelet Galerkin method with N degrees of freedom in log-price space. The dense matrix for ${\mathcal{A}}$ 
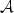can be replaced by a sparse matrix in the wavelet basis, and the linear systemsin each implicit time step are solved approximativelywith GMRES in linear complexity. The total work of the algorithm for M time steps is bounded byO(MN(log(N))2) operations and O(Nlog(N)) memory.The deterministic algorithm gives optimal convergence rates (up to logarithmic terms) for the computed solutionin the same complexity as finite difference approximationsof the standard Black–Scholes equation.Computational examples for various Lévy price processes are presented.
