1 results
Invariance principles in queueing theory
-
- Journal:
- Journal of Applied Probability / Volume 26 / Issue 4 / December 1989
- Published online by Cambridge University Press:
- 14 July 2016, pp. 845-857
- Print publication:
- December 1989
-
- Article
- Export citation
-
Several stochastic processes in queueing theory are based upon compound renewal processes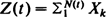
. For queues in light traffic, however, the summands {Xk}and the renewal counting process {N(t)} are typically dependent on each other. Making use of recent invariance principles for such situations, we present some weak and strong approximations for the GI/G/1 queues in light and heavy traffic. Some applications are discussed including convergence rate statements or Darling–Erdös-type extreme value theorems for the processes under consideration.
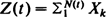. For queues in light traffic, however, the summands {