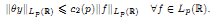1 results
Weighted Estimates for Solutions of the General Sturm-Liouville Equation and the Everitt-Giertz Problem. I
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 21 July 2014, pp. 125-147
-
- Article
- Export citation
-
Consider the equation
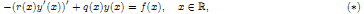
where ƒ ∈ Lp(ℝ), p ∈ (1, ∞) and
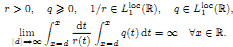
By a solution of (*), we mean any function y absolutely continuous together with (ry′) and satisfying (*) almost everywhere on ℝ. In addition, we assume that (*) is correctly solvable in the space Lp(ℝ), i.e.
(1) for any function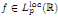
, there exists a unique solution y ∈ Lp(ℝ) of (*);(2) there exists an absolute constant c1(p) > 0 such that the solution y ∈ Lp(ℝ) of (*) satisfies the inequality
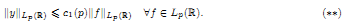
We study the following problem on the strengthening estimate (**). Let a non-negative function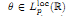
be given. We have to find minimal additional restrictions for θ under which the following inequality holds:
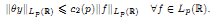
Here, y is a solution of (*) from the class Lp(ℝ), and c2 (p) is an absolute positive constant.
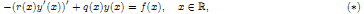
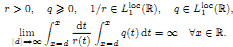
, there exists a unique solution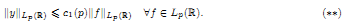 
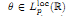be given. We have to find minimal additional restrictions for 
