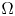This note studies local integral gradient bounds for distributional solutions of a large class of partial differential inequalities with diffusion in divergence form and power-like first-order terms. The applications of these estimates are two-fold. First, we show the (sharp) global Hölder regularity of distributional semi-solutions to this class of diffusive PDEs with first-order terms having supernatural growth and right-hand side in a suitable Morrey class posed on a bounded and regular open set $\Omega$. Second, we provide a new proof of entire Liouville properties for inequalities with superlinear first-order terms without assuming any one-side bound on the solution for the corresponding homogeneous partial differential inequalities. We also discuss some extensions of the previous properties to problems arising in sub-Riemannian geometry and also to partial differential inequalities posed on noncompact complete Riemannian manifolds under appropriate area-growth conditions of the geodesic spheres, providing new results in both these directions. The methods rely on integral arguments and do not exploit maximum and comparison principles.

Structural changes of the pore space and clogging phenomena are inherent to many porous media applications. However, related analytical investigations remain challenging due to potentially vanishing coefficients in the respective systems of partial differential equations. In this research, we apply an appropriate scaling of the unknowns and work with porosity-weighted function spaces. This enables us to prove existence, uniqueness and non-negativity of weak solutions to a combined flow and transport problem with vanishing, but prescribed porosity field, permeability and diffusion.