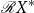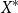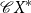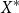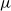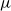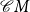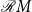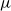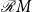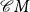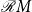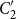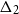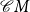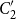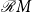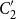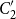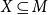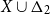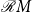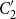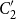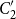The family
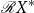 ${\mathcal{R}} X^*$
of regular subsets of the free monoid
${\mathcal{R}} X^*$
of regular subsets of the free monoid
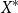 $X^*$
generated by a finite set X is the standard example of a
$X^*$
generated by a finite set X is the standard example of a
 ${}^*$
-continuous Kleene algebra. Likewise, the family
${}^*$
-continuous Kleene algebra. Likewise, the family
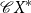 ${\mathcal{C}} X^*$
of context-free subsets of
${\mathcal{C}} X^*$
of context-free subsets of
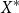 $X^*$
is the standard example of a
$X^*$
is the standard example of a
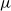 $\mu$
-continuous Chomsky algebra, i.e. an idempotent semiring that is closed under a well-behaved least fixed-point operator
$\mu$
-continuous Chomsky algebra, i.e. an idempotent semiring that is closed under a well-behaved least fixed-point operator
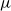 $\mu$
. For arbitrary monoids M,
$\mu$
. For arbitrary monoids M,
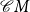 ${\mathcal{C}} M$
is the closure of
${\mathcal{C}} M$
is the closure of
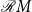 ${\mathcal{R}}M$
as a
${\mathcal{R}}M$
as a
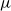 $\mu$
-continuous Chomsky algebra, more briefly, the fixed-point closure of
$\mu$
-continuous Chomsky algebra, more briefly, the fixed-point closure of
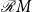 ${\mathcal{R}} M$
. We provide an algebraic representation of
${\mathcal{R}} M$
. We provide an algebraic representation of
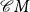 ${\mathcal{C}} M$
in a suitable product of
${\mathcal{C}} M$
in a suitable product of
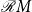 ${\mathcal{R}} M$
with
${\mathcal{R}} M$
with
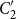 $C_2'$
, a quotient of the regular sets over an alphabet
$C_2'$
, a quotient of the regular sets over an alphabet
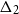 $\Delta_2$
of two pairs of bracket symbols. Namely,
$\Delta_2$
of two pairs of bracket symbols. Namely,
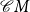 ${\mathcal{C}}M$
is isomorphic to the centralizer of
${\mathcal{C}}M$
is isomorphic to the centralizer of
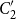 $C_2'$
in the product of
$C_2'$
in the product of
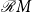 ${\mathcal{R}} M$
with
${\mathcal{R}} M$
with
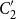 $C_2'$
, i.e. the set of those elements that commute with all elements of
$C_2'$
, i.e. the set of those elements that commute with all elements of
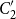 $C_2'$
. This generalizes a well-known result of Chomsky and Schützenberger (1963, Computer Programming and Formal Systems, 118–161) and admits us to denote all context-free languages over finite sets
$C_2'$
. This generalizes a well-known result of Chomsky and Schützenberger (1963, Computer Programming and Formal Systems, 118–161) and admits us to denote all context-free languages over finite sets
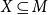 $X\subseteq M$
by regular expressions over
$X\subseteq M$
by regular expressions over
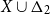 $X\cup\Delta_2$
interpreted in the product of
$X\cup\Delta_2$
interpreted in the product of
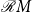 ${\mathcal{R}} M$
and
${\mathcal{R}} M$
and
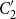 $C_2'$
. More generally, for any
$C_2'$
. More generally, for any
 ${}^*$
-continuous Kleene algebra K the fixed-point closure of K can be represented algebraically as the centralizer of
${}^*$
-continuous Kleene algebra K the fixed-point closure of K can be represented algebraically as the centralizer of
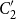 $C_2'$
in the product of K with
$C_2'$
in the product of K with
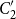 $C_2'$
.
$C_2'$
.