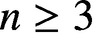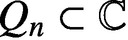For $n\geq 3$ , let $Q_n\subset \mathbb {C}$ be an arbitrary regular n-sided polygon. We prove that the Cauchy transform $F_{Q_n}$ of the normalised two-dimensional Lebesgue measure on $Q_n$ is univalent and starlike but not convex in $\widehat {\mathbb {C}}\setminus Q_n$ .

In this paper we determine the ${{L}^{1}}\to {{L}^{1}}$ and ${{L}^{\infty }}\to {{L}^{\infty }}$ norms of an integral operator $\mathcal{N}$ related to the gradient of the solution of Poisson equation in the unit ball with vanishing boundary data in sense of distributions.

We prove that if Ω is a simply connected quadrature domain (QD) of a distribution with compact support and the point of infinity belongs to the boundary, then the boundary has an asymptotic curve that is a straight line, parabola or infinite ray. In other words, such QDs in the plane are perturbations of null QDs.

In this paper a $T(1)$ theorem for Calder\'on--Zygmund operators (CZOs) valid for non-doubling measures with atoms is proved. In the classical Calder\'on--Zigmund theory an essential assumption is the doubling property of the underlying measure $\mu$ in ${\mathbb R}^n$. Some recent results have shown that a big part of the classical theory can be extended to the case of non-doubling measures, with only some mild `growth' condition on the measure $\mu$. In the particular case of the Cauchy transform $Cf(x) = \int f(y)/(y-x) \, d\mu(y)$, the main result of the paper can be stated easily: the Cauchy transform is bounded in $L^2(\mu)$ if and only if it is bounded in $L^2(\mu)$ over characteristic functions of squares. The proof of the main result is based on the use of the Haar basis with random dyadic lattices, following an idea of Nazarov, Treil and Volberg (`Cauchy integral and Calder\'on--Zygmund operators on nonhomogeneous spaces', {\em Internat. Math. Res. Notices} (1997) 15, 703--726), where a $T(1)$ theorem for non-doubling continuous measures was obtained. The case of a measure $\mu$ with atoms studied in the present paper is quite different from the case of continuous measures. For example, if $\mu$ has atoms, the $L^2(\mu)$ boundedness of a CZO does not imply its $L^p(\mu)$ boundedness for some $p\neq2$. The differences arise because a measure $\mu$ with atoms does not satisfy the essential `growth' condition that is involved in the arguments for proving the $L^2$ boundedness of CZOs for continuous measures. 2000 Mathematics Subject Classification: 42B20.