A Cantor series expansion for a real number x with respect to a basic sequence 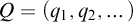 $Q=(q_1,q_2,\dots )$
, where
$Q=(q_1,q_2,\dots )$
, where 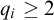 $q_i \geq 2$
, is a generalization of the base b expansion to an infinite sequence of bases. Ki and Linton in 1994 showed that for ordinary base b expansions the set of normal numbers is a
$q_i \geq 2$
, is a generalization of the base b expansion to an infinite sequence of bases. Ki and Linton in 1994 showed that for ordinary base b expansions the set of normal numbers is a 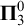 $\boldsymbol {\Pi }^0_3$
-complete set, establishing the exact complexity of this set. In the case of Cantor series there are three natural notions of normality: normality, ratio normality, and distribution normality. These notions are equivalent for base b expansions, but not for more general Cantor series expansions. We show that for any basic sequence the set of distribution normal numbers is
$\boldsymbol {\Pi }^0_3$
-complete set, establishing the exact complexity of this set. In the case of Cantor series there are three natural notions of normality: normality, ratio normality, and distribution normality. These notions are equivalent for base b expansions, but not for more general Cantor series expansions. We show that for any basic sequence the set of distribution normal numbers is  $\boldsymbol {\Pi }^0_3$
-complete, and if Q is
$\boldsymbol {\Pi }^0_3$
-complete, and if Q is 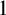 $1$
-divergent then the sets of normal and ratio normal numbers are
$1$
-divergent then the sets of normal and ratio normal numbers are 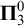 $\boldsymbol {\Pi }^0_3$
-complete. We further show that all five non-trivial differences of these sets are
$\boldsymbol {\Pi }^0_3$
-complete. We further show that all five non-trivial differences of these sets are 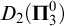 $D_2(\boldsymbol {\Pi }^0_3)$
-complete if
$D_2(\boldsymbol {\Pi }^0_3)$
-complete if 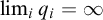 $\lim _i q_i=\infty $
and Q is
$\lim _i q_i=\infty $
and Q is 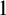 $1$
-divergent. This shows that except for the trivial containment that every normal number is ratio normal, these three notions are as independent as possible.
$1$
-divergent. This shows that except for the trivial containment that every normal number is ratio normal, these three notions are as independent as possible.