We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper, we study the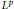 
${{L}^{p}}$ mapping properties of a class of singular integral operators with rough kernels belonging to certain block spaces. We prove that our operators are bounded on 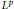${{L}^{p}}$ provided that their kernels satisfy a size condition much weaker than that for the classical Calderón–Zygmund singular integral operators. Moreover, we present an example showing that our size condition is optimal. As a consequence of our results, we substantially improve a previously known result on certain maximal functions.
