Reverse Mathematics (RM) is a program in the foundations of mathematics where the aim is to find the minimal axioms needed to prove a given theorem of ordinary mathematics. Generally, the minimal axioms are equivalent to the theorem at hand, assuming a weak logical system called the base theory. Moreover, many theorems are either provable in the base theory or equivalent to one of four logical systems, together called the Big Five. For instance, the Weierstrass approximation theorem, i.e., that a continuous function can be approximated uniformly by a sequence of polynomials, has been classified in RM as being equivalent to weak König’s lemma, the second Big Five system. In this paper, we study approximation theorems for discontinuous functions via Bernstein polynomials from the literature. We obtain many equivalences between the latter and weak König’s lemma. We also show that slight variations of these approximation theorems fall far outside of the Big Five but fit in the recently developed RM of new ‘big’ systems, namely the uncountability of 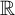 ${\mathbb R}$, the enumeration principle for countable sets, the pigeon-hole principle for measure, and the Baire category theorem.
${\mathbb R}$, the enumeration principle for countable sets, the pigeon-hole principle for measure, and the Baire category theorem.