We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let R be a commutative Noetherian ring with nonzero identity and let M be a finitely generated R-module. In this paper, we prove that if an ideal I of R is generated by a u.s.d-sequence on M then the local cohomology module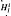 
(M) is I-cofinite. Furthermore, for any system of ideals Φ of R, we study the cofiniteness problem in the context of general local cohomology modules.
