This work investigates heat transport in rotating internally heated convection, for a horizontally periodic fluid between parallel plates under no-slip and isothermal boundary conditions. The main results are the proof of lower bounds on the mean temperature, $\overline {{\langle {T} \rangle }}$, and the heat flux out of the bottom boundary, ${\mathcal {F}}_B$, at infinite Prandtl number, where the Prandtl number is the non-dimensional ratio of viscous to thermal diffusion. The lower bounds are functions of the Rayleigh number quantifying the ratio of internal heating to diffusion and the Ekman number, $E$, which quantifies the ratio of viscous diffusion to rotation. We utilise two different estimates on the vertical velocity, $w$, one pointwise in the domain (Yan, J. Math. Phys., vol. 45(7), 2004, pp. 2718–2743) and the other an integral estimate over the domain (Constantin et al., Phys. D: Non. Phen., vol. 125, 1999, pp. 275–284), resulting in bounds valid for different regions of buoyancy-to-rotation dominated convection. Furthermore, we demonstrate that similar to rotating Rayleigh–Bénard convection, for small $E$, the critical Rayleigh number for the onset of convection asymptotically scales as $E^{-4/3}$.

Rotating convection is considered on the tilted $f$-plane where gravity and rotation are not aligned. For sufficiently large rotation rates, $\Omega$, the Taylor–Proudman effect results in the gyroscopic alignment of anisotropic columnar structures with the rotation axis giving rise to rapidly varying radial length scales that vanishes as $\Omega ^{-1/3}$ for $\Omega \rightarrow \infty$. Compounding this phenomenon is the existence of viscous (Ekman) layers adjacent to the impenetrable bounding surfaces that scale as $\Omega ^{-1/2}$. In this investigation, these constraints are relaxed upon utilising a non-orthogonal coordinate representation of the fluid equations where the upright coordinate aligns with rotation axis. This exposes the problem to asymptotic perturbation methods that permit: (i) relaxation of the constraints of gyroscopic alignment; (ii) the filtering of Ekman layers through the uncovering of parameterised velocity pumping boundary conditions; and (iii) the development of reduced quasi-geostrophic systems valid in the limit $\Omega \rightarrow \infty$. Linear stability investigations reveal excellent quantitative agreement between results from parameterised or unapproximated mechanical boundary conditions. For no-slip boundaries, it is demonstrated that the associated Ekman pumping alters convective onset through an enhanced destabilisation of large spatial scales. The range of unstable modes at a fixed thermal forcing is thus significantly extended with a direct dependence on $\Omega$. This holds true even for geophysical and astrophysical regimes characterised by extreme values of the non-dimensional Ekman number $E$. The nonlinear regime is explored via the global heat and momentum transport of single-mode solutions to the quasi-geostrophic systems which indicate $O(1)$ changes which do not scale with the size of $E$.

We report an experimental study of Rayleigh–Bénard convection of liquid metal GaInSn in a cuboid cell with an aspect ratio of 0.5 under the effect of a horizontal magnetic field. The Rayleigh number spans a range of $3.8\times 10^5 \leqslant Ra \leqslant 1.1\times 10^7$, while the magnetic field strength reaches up to 0.5 T, corresponding to a maximum Hartmann number to 2041. By combining temperature and velocity measurements, we identify several flow morphologies, including a novel cellular pattern characterized by four stacked vortices that periodically squeeze and induce velocity reversals. Based on the identified flow morphologies, we partition the entire ($Ra, Ha$) parameter space into five distinct flow regimes and systematically investigate the flow characteristics within each regime. The temperature gradient and oscillation frequency exhibit scaling relationships with the combined parameters $Ra$ and $Ha$. Notably, we observe a coupling between flow regime and global transport efficiencies, particularly in a regime dominated by the double-roll structure, which experiences a maximum 36 % decrease in heat transfer efficiency compared with the single-roll structure. The dependencies of heat and momentum transport on $Ra$ and $Ha$ follow scaling laws as $Nu \sim (Ha^{-2/3}RaPr^{-1})^{3/5}$ and $Re \sim (Ha^{-1}RaPr^{-1})^{4/3}$, respectively.

We employ direct numerical simulations to investigate the heat transfer and flow structures in turbulent Rayleigh–Bénard convection in both cylindrical cells and laterally periodic domains, spanning an unprecedentedly wide range of aspect ratios $0.075 \leqslant \varGamma \leqslant 32$. We focus on Prandtl number ${Pr}=1$ and Rayleigh numbers ${{Ra}}=2\times 10^7$ and ${{Ra}}=10^8$. In both cases, with increasing aspect ratio, the heat transfer first increases, then reaches a maximum (which is more pronounced for the cylindrical case due to confinement effects), and then slightly goes down again before it finally saturates at the large aspect ratio limit, which is achieved already at $\varGamma \approx 4$. Already for $\varGamma \gtrsim 0.75$, the heat transfers in both cylindrical and laterally periodic domains become identical. The large-$\varGamma$ limit for the volume-integrated Reynolds number and the boundary layer thicknesses are also reached at $\varGamma \approx 4$. However, while the integral flow properties converge at $\varGamma \approx 4$, the confinement of a cylindrical domain impacts the temperature and velocity variance distributions up to $\varGamma \approx 16$, as thermal superstructures cannot form close to the sidewall.

Direct numerical simulation (DNS) is performed to explore turbulent Rayleigh–Bénard convection in spherical shells. Our simulations cover six distinct values of radius ratio, 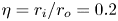$\eta = r_i/r_o = 0.2$, 0.3, 0.4, 0.5, 0.6 and 0.8, under the assumption of a centrally condensed mass with gravity profile 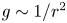$g \sim 1/r^{2}$; where 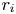$r_i$, 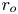$r_o$ and 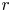$r$ denote the inner shell radius, the outer shell radius and the local radial coordinate, respectively. The Prandtl number is kept constant at unity while the Rayleigh number (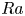$Ra$) is varied from 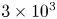$3 \times 10^{3}$ to 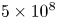$5 \times 10^8$. Our primary aim is to analyze how the radius ratio influences the global transport properties and flow physics. To gain insights into the scaling behaviour of the Nusselt number ($Nu$) and the Reynolds number (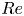$Re$) with respect to 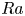$Ra$ and 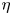$\eta$, we apply the Grossmann–Lohse (GL) theory (Grossmann & Lohse, J. Fluid Mech., vol. 407, 2000, pp. 27–56) to the system. It is observed that the scaling exponents for 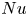$Nu$ and 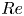$Re$ in relation to 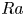$Ra$ are more significant for smaller 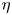$\eta$ values, suggesting that the simulations with smaller 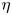$\eta$ reach the classical 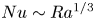$Nu\sim Ra^{1/3}$ regime at a relatively lower 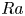$Ra$. This observation could also imply the systems with smaller 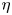$\eta$ might transition to the ultimate regime earlier at a smaller 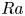$Ra$. Based on our extensive DNS data, we establish that the thickness of the inner thermal boundary, 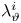$\lambda _{\vartheta }^{i}$, follows a scaling relationship of 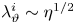$\lambda _{\vartheta }^{i} \sim \eta ^{1/2}$. This relationship, in turn, leads to a scaling law for 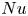$Nu$ in the form of 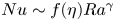$Nu \sim f(\eta ) Ra^{\gamma }$, where the function 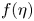$f(\eta )$ is defined as 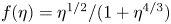$f(\eta ) = {\eta ^{1/2}}/{(1+\eta ^{4/3})}$, and the exponent 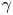$\gamma$ depends on both 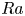$Ra$ and 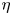$\eta$. Additionally, we characterize and explain the asymmetry in the velocity field by introducing the separate Reynolds numbers for the inner and outer shells. The asymmetry of the kinetic and thermal energy dissipation rates in the inner and outer boundary layers (BLs) is also quantified.

We study the effect of geometrical confinement on thermal convection by laboratory experiments and direct numerical simulations using Hele-Shaw geometries (typically the gap-to-height aspect ratio $0.12$) for the Prandtl number $Pr \geq 40$ and the Rayleigh number $Ra \leq 6 \times 10^7$. Under such strong unidirectional confinement, the convective flows are forced to squeeze within the narrow gap and exhibit unique spatiotemporal signatures, which contrast those in unconfined systems. With the increase of $Ra$, we identify that the system experiences five convective regimes that can be classified from two aspects, time dependency and flow dimensionality: (I) quasi-two-dimensional (quasi-2-D) steady flow; (II) quasi-2-D flow with oscillatory corner rolls; (III) three-dimensional (3-D) flow with oscillatory corner rolls; (IV) 3-D steady flow; and (V) 3-D time-dependent motion of plumes around sidewalls. Notably, unsteadiness does not emerge globally, but is localised near the sidewalls as oscillatory corner rolls, resulting in the regime transitions happening in a quasi-steady manner. We confirm that these regime transitions show less dependence on both $Pr$ and the other (wider) horizontal scale of the geometry. Moreover, we find that a recently proposed criterion ‘degree of confinement’ (Noto et al., Proc. Natl Acad. Sci. USA, vol. 121, issue 28, 2024, e2403699121) successfully explains the emergence of 3-D structures, expanding its applicable range to smaller $Ra$. This study deepens the comprehension of the thermal convection emerging in tight geometries, impacting across disciplines, such as Earth and planetary science, and thermal engineering.

The paper by Castaing et al. (J. Fluid Mech., vol. 204, 1989, pp. 1–30) on turbulent Rayleigh–Bénard convection has been one of the most impactful papers on the subject – not by giving the right and complete answers but by developing versatile concepts and by asking the right questions, namely: (i) What is the overall flow organization? (ii) What is the dependence of the Nusselt number ${\textit {Nu}}$ (the dimensionless heat transport) on the Rayleigh number ${\textit {Ra}}$ (the thermal driving strength)? (iii) What is the ultimate state of turbulence for extremely large ${\textit {Ra}}$? Thanks to Castaing et al. having asked the right questions, the field has made tremendous progress over the last 35 years.

Bounds on heat transfer have been the subject of previous studies concerning convection in the Boussinesq approximation: in the Rayleigh–Bénard configuration, the first result obtained by Howard (J. Fluid Mech., vol. 17, issue 3, 1963, pp. 405–432) states that the dimensionless heat flux $\textit {Nu}$ carried out by convection is such that $\textit {Nu} < (3/64 \ Ra)^{1/2}$ for large values of the Rayleigh number $Ra$, independently of the Prandtl number $Pr$. This is still the best-known upper bound, only with the prefactor improved to $\textit {Nu} -1 < 0.02634 \ Ra^{1/2}$ by Plasting & Kerswell (J. Fluid Mech., vol. 477, 2003, pp. 363–379). In the present paper, this result is extended to compressible convection. An upper bound is obtained for the anelastic liquid approximation, which is similar to an anelastic model used in astrophysics based on a turbulent diffusivity for entropy. The anelastic bound is still scaling as $Ra^{1/2}$, independently of $Pr$, but depends on the dissipation number $\mathcal {D}$ and on the equation of state. For monatomic gases and large Rayleigh numbers, the bound is $\textit {Nu} < 25.8\, Ra^{{1}/{2}} / (1-\mathcal {D}/2 )^{{5}/{2}}$.

We report on Lagrangian statistics of turbulent Rayleigh–Bénard convection under very different conditions. For this, we conducted particle tracking experiments in a $H=1.1$-m-high cylinder of aspect ratio $\varGamma =1$ filled with air (Pr = 0.7), as well as in two rectangular cells of heights $H=0.02$ m ($\varGamma =16$) and $H=0.04$ m ($\varGamma =8$) filled with water (Pr = 7.0), covering Rayleigh numbers in the range $10^6\le {\textit {Ra}}\le 1.6\times 10^9$. Using the Shake-The-Box algorithm, we have tracked up to 500 000 neutrally buoyant particles over several hundred free-fall times for each set of control parameters. We find the Reynolds number to scale at small Ra (large Pr) as $ {\textit{Re}} \propto {\textit{Ra}}^{0.6}$. Further, the averaged horizontal particle displacement is found to be universal and exhibits a ballistic regime at small times and a diffusive regime at larger times, for sufficiently large $\varGamma$. The diffusive regime occurs for time lags larger than $\tau _{co}$, which is the time scale related to the decay of the velocity autocorrelation. Compensated as $\tau _{co} {\textit {Pr}}^{-0.3}$, this time scale is universal and rather independent of $ {\textit {Ra}}$ and $\varGamma$. We have also investigated the Lagrangian velocity structure function $S^2_i(\tau )$, which is dominated by viscous effects for times smaller than the Kolmogorov time $\tau _\eta$ and hence $S^2_i\propto \tau ^2$. For larger times we find a novel scaling for the different components with exponents smaller than what is expected in the inertial range of homogeneous isotropic turbulence without buoyancy. Studying particle-pair dispersion, we find a Batchelor scaling (${\propto }\,t^2$) on small time scales, diffusive scaling (${\propto }\,t$) on large time scales and Richardson-like scaling (${\propto }\,t^3$) for intermediate time scales.

Radial unstable stratification is a potential source of turbulence in the cold regions of accretion disks. To investigate this thermal effect, here we focus on two-dimensional Rayleigh–Bénard convection in an annulus subject to radially dependent gravitational acceleration $g \propto 1/r$. Next to the Rayleigh number $Ra$ and Prandtl number $Pr$, the radius ratio $\eta$, defined as the ratio of inner and outer cylinder radii, is a crucial parameter governing the flow dynamics. Using direct numerical simulations for $Pr=1$ and $Ra$ in the range from $10^7$ to $10^{10}$, we explore how variations in $\eta$ influence the asymmetry in the flow field, particularly in the boundary layers. Our results show that in the studied parameter range, the flow is dominated by convective rolls and that the thermal boundary-layer (TBL) thickness ratio between the inner and outer boundaries varies as $\eta ^{1/2}$. This scaling is attributed to the equality of velocity scales in the inner ($u_i$) and outer ($u_o$) regions. We further derive that the temperature drops in the inner and outer TBLs scale as $1/(1+\eta ^{1/2})$ and $\eta ^{1/2}/(1+\eta ^{1/2})$, respectively. The scalings and the temperature drops are in perfect agreement with the numerical data.

Unlike in solids, heat transfer in fluids can be greatly enhanced due to the presence of convection. Under gravity, an unevenly distributed temperature field results in differences in buoyancy, driving fluid motion that is seen in Rayleigh–Bénard convection (RBC). In RBC, the overall heat flux is found to have a power-law dependence on the imposed temperature difference, with enhanced heat transfer much beyond thermal conduction. In a bounded domain of fluid such as a cube, how RBC responds to thermal perturbations from the vertical sidewall is not clear. Will sidewall heating or cooling modify flow circulation and heat transfer? We address these questions experimentally by adding heat to one side of the RBC. Through careful flow, temperature and heat flux measurements, the effects of adding side heating to RBC are examined and analysed, where a further enhancement of flow circulation and heat transfer is observed. Our results also point to a direct and simple control of the classical RBC system, allowing further manipulation and control of thermal convection through sidewall conditions.

Turbulent convection in the interiors of the Sun and the Earth occurs at high Rayleigh numbers $Ra$, low Prandtl numbers $Pr$, and different levels of rotation rates. To understand the combined effects better, we study rotating turbulent convection for $Pr = 0.021$ (for which some laboratory data corresponding to liquid metals are available), and varying Rossby numbers $Ro$, using direct numerical simulations in a slender cylinder of aspect ratio 0.1; this confinement allows us to attain high enough Rayleigh numbers. We are motivated by the earlier finding in the absence of rotation that heat transport at high enough $Ra$ is similar between confined and extended domains. We make comparisons with higher aspect ratio data where possible. We study the effects of rotation on the global transport of heat and momentum as well as flow structures (a) for increasing rotation at a few fixed values of $Ra$, and (b) for increasing $Ra$ (up to $10^{10}$) at the fixed, low Ekman number $1.45 \times 10^{-6}$. We compare the results with those from unity $Pr$ simulations for the same range of $Ra$ and $Ro$, and with the non-rotating case over the same range of $Ra$ and low $Pr$. We find that the effects of rotation diminish with increasing $Ra$. These results and comparison studies suggest that for high enough $Ra$, rotation alters convective flows in a similar manner for small and large aspect ratios, so useful insights on the effects of high thermal forcing on convection can be obtained by considering slender domains.

This study explores heat and turbulent modulation in three-dimensional multiphase Rayleigh–Bénard convection using direct numerical simulations. Two immiscible fluids with identical reference density undergo systematic variations in dispersed-phase volume fractions, $0.0 \leq \varPhi \leq 0.5$, and ratios of dynamic viscosity, $\lambda _{\mu }$, and thermal diffusivity, $\lambda _{\alpha }$, within the range $[0.1\unicode{x2013}10]$. The Rayleigh, Prandtl, Weber and Froude numbers are held constant at $10^8$, $4$, $6000$ and $1$, respectively. Initially, when both fluids share the same properties, a 10 % Nusselt number increase is observed at the highest volume fractions. In this case, despite a reduction in turbulent kinetic energy, droplets enhance energy transfer to smaller scales, smaller than those of single-phase flow, promoting local mixing. By varying viscosity ratios, while maintaining a constant Rayleigh number based on the average mixture properties, the global heat transfer rises by approximately 25 % at $\varPhi =0.2$ and $\lambda _{\mu }=10$. This is attributed to increased small-scale mixing and turbulence in the less viscous carrier phase. In addition, a dispersed phase with higher thermal diffusivity results in a 50 % reduction in the Nusselt number compared with the single-phase counterpart, owing to faster heat conduction and reduced droplet presence near walls. The study also addresses droplet-size distributions, confirming two distinct ranges dominated by coalescence and breakup with different scaling laws.

We studied the transport and deposition behaviour of point particles in Rayleigh–Bénard convection cells subjected to Couette-type wall shear. Direct numerical simulations (DNSs) are performed for Rayleigh number ($Ra$) in the range $10^{7} \leq Ra \leq ~10^9$ with a fixed Prandtl number $Pr = 0.71$, while the wall-shear Reynolds number ($Re_w$) is in the range $0 \leq Re_w \leq ~12\,000$. With the increase of $Re_w$, the large-scale rolls expanded horizontally, evolving into zonal flow in two-dimensional simulations or streamwise-oriented rolls in three-dimensional simulations. We observed that, for particles with a small Stokes number ($St$), they either circulated within the large-scale rolls when buoyancy dominated or drifted near the walls when shear dominated. For medium $St$ particles, pronounced spatial inhomogeneity and preferential concentration were observed regardless of the prevailing flow state. For large $St$ particles, the turbulent flow structure had a minor influence on the particles’ motion; although clustering still occurred, wall shear had a negligible influence compared with that for medium $St$ particles. We then presented the settling curves to quantify the particle deposition ratio on the walls. Our DNS results aligned well with previous theoretical predictions, which state that small $St$ particles settle with an exponential deposition ratio and large $St$ particles settle with a linear deposition ratio. For medium $St$ particles, where complex particle–turbulence interaction emerges, we developed a new model describing the settling process with an initial linear stage followed by a nonlinear stage. Unknown parameters in our model can be determined either by fitting the settling curves or using empirical relations. Compared with DNS results, our model also accurately predicts the average residence time across a wide range of $St$ for various $Re_w$.

In the generalized quasilinear approximation (GQLA) (Marston et al., Phys. Rev. Lett., vol. 116, 2016, 214501), a threshold wavenumber ($k_0$) in the direction of translational symmetry segregates the total into large- ($l$) and small-scale ($h$) fields. While the governing equation for the large-scale field is fully nonlinear, that for the small scales is linearized with respect to the large-scale field. In addition, some nonlinear triad interactions are omitted in the GQLA. Herein, the GQLA is applied to two-dimensional planar Rayleigh–Bénard convection (RBC). A scale separation between the large-scale convection rolls and small-scale turbulent fluctuations is typical in RBC. The present work explores the efficacy of GQLA in capturing the scale-by-scale energy transfer processes in RBC. The initial condition for the GQLA simulations was either the statistically stationary state obtained in direct numerical simulation (DNS) or random fluctuations superimposed on the linear conductive temperature profile and $\boldsymbol {u}=0$. The GQLA simulations can capture the convection rolls for $k_0$ larger than or equal to the dominant wavenumber for thermal driving of the flow ($k_0 \ge k_{\hat {Q}}$). Additionally, the GQLA emulates the fully nonlinear dynamics for $k_0$ larger than or equal to the first harmonic of the convection-roll wavenumber ($k_0 \ge 2k_{roll}$). In the intermediate regime with $2k_{roll} > k_0 \ge k_{\hat {Q}}$, the dynamics captured in GQLA simulations is different from the DNS. In DNS, two primary energy transfer processes dominate: (i) the energy transfer to/from the convection rolls and (ii) the scale-by-scale inverse kinetic energy and forward thermal energy cascades mediated by the convection rolls. The fully nonlinear dynamics is emulated by GQLA when these energy transfer processes are faithfully reproduced. Utilizing the framework of altering the triad interactions in GQLA, an additional intrusive calculation, including target triad interactions, is performed here to study their influence. This intrusive calculation shows that the convection rolls are not captured in GQLA for $k_0 < k_{\hat {Q}}$ because of the exclusion of the $h \to l \to l$ and $l \to h \to h$ triad interactions in GQLA. The inclusion of these triad interactions in the intrusive calculation yields the convection rolls, and the reproduced dynamics is similar to that of the intermediate GQLA regime with $2k_{roll} > k_0 \ge k_{\hat {Q}}$.

We discuss the applicability of quasilinear-type approximations for a turbulent system with a large range of spatial and temporal scales. We consider a paradigm fluid system of rotating convection with vertical and horizontal temperature gradients. In particular, the interaction of rotation with the horizontal temperature gradient drives a ‘thermal wind’ shear flow whose strength is controlled by the horizontal temperature gradient. Varying this parameter therefore systematically alters the ordering of the shearing time scale, the convective time scale and the correlation time scale. We demonstrate that quasilinear-type approximations work well when the shearing time scale or the correlation time scale is sufficiently short. In all cases, the generalised quasilinear approximation systematically outperforms the quasilinear approximation. We discuss the consequences for statistical theories of turbulence interacting with mean gradients.

We study the effects of Prandtl number $\mathit {Pr}$ and Rayleigh number $\mathit {Ra}$ in two-dimensional Rayleigh–Bénard convection without boundaries, i.e. with periodic boundary conditions. For Prandtl numbers in the range $10^{-3} \leqslant \mathit {Pr} \leqslant 10^2$, the viscous dissipation scales as $\epsilon _\nu \propto \mathit {Pr}^{1/2}\mathit {Ra}^{-1/4}$, which is based on the observation that enstrophy $\langle {\omega ^2}\rangle \propto \mathit {Pr}^0 \mathit {Ra}^{1/4}$, and the Nusselt number tends to follow the ‘ultimate’ scaling $\mathit {Nu} \propto \mathit {Pr}^{1/2}\mathit {Ra}^{1/2}$ for all values of $\mathit {Pr}$ considered. The inverse cascade of kinetic energy forms the power-law spectrum $\hat {E}_u(k) \propto k^{-2.3}$, which is close to $k^{-11/5}$ proposed by the Bolgiano–Obukhov (BO) scaling. The potential energy flux is not constant, in contrast to one of the main assumptions underlying the BO phenomenology. So, the direct cascade of potential energy forms the power-law spectrum $\hat {E}_\theta (k) \propto k^{-1.2}$, which deviates from the expected $k^{-7/5}$. Finally, at $\mathit {Pr} \to 0$ and $\infty$, we find that the dynamics is dominated by vertically oriented elevator modes that grow without bound, even at high Rayleigh numbers and with large-scale dissipation present.

Melting and solidification in periodically time-modulated thermal convection are relevant for numerous natural and engineering systems, for example, glacial melting under periodic sun radiation and latent thermal energy storage under periodically pulsating heating. It is highly relevant for the estimation of melt rate and melt efficiency management. However, even the dynamics of a solid–liquid interface shape subjected to a simple sinusoidal heating has not yet been investigated in detail. In this paper, we offer a better understanding of the modulation frequency dependence of the melting and solidification front. We numerically investigate periodic melting and solidification in turbulent convective flow with the solid above and the melted liquid below, and sinusoidal heating at the bottom plate with the mean temperature equal to the melting temperature. We investigate how the periodic heating can prevent the full solidification, and the resulting flow structures and the quasi-equilibrium interface height. We further study the dependence on the heating modulation frequency. As the frequency decreases, we found two distinct regimes, which are ‘partially solid’ and ‘fully solid’. In the fully solid regime, the liquid freezes completely, and the effect of the modulation is limited. In the partially solid regime, the solid partially melts, and a steady or unsteady solid–liquid interface forms depending on the frequency. The interface height can be derived based on the energy balance through the interface. In the partially solid regime, the interface height oscillates periodically, following the frequency of modulation. Here, we propose a perturbation approach that can predict the dependency of the oscillation amplitude on the modulation frequency.

In a horizontally heated melting system, where a solid substance is subject to melting by a warmer liquid beneath, the presence of solute in the liquid introduces a complex interplay between temperature and concentration dynamics. Employing a recently developed sharp interface method (Xue et al., J. Comput. Phys., vol. 491, 2023), we conduct direct numerical simulations to investigate the transient behaviour of the system across a broad range of Rayleigh numbers and solute concentrations. Our observations reveal distinct flow regimes: at low concentrations, the system resembles a temperature-driven melting problem, characterized by vortex rolls beneath the melting interface. As the solute concentration increases, a stably stratified layer emerges beneath the interface, leading to the transition from thermal convection to penetrative convection, which resembles those flow characteristics observed in the double-diffusive convection. This shift results from the competition between the stabilizing effect induced by solute concentration gradient and the destabilizing effect caused by temperature gradient. Otherwise in the diffusion regime, characterized by very high solute concentrations, the flow becomes static due to the complete suppression of convection by the stably stratified layer. This regime further exhibits two distinct patterns: ‘melting’ and ‘dissolution’. Beyond characterizing diverse flow patterns, our study conducts a quantitative analysis, examining heat/mass transfer, melting rates, and the evolution of temperature and concentration at the interface. These insights contribute to a better understanding of the intricate interplay between temperature and solute concentration during phase change, with implications for accurately estimating melting rates in binary fluid systems.

Rayleigh–Bénard convection in a rotating spherical shell provides a simplified model for convective dynamics of planetary and stellar interiors. Over the past decades, the problem has been studied extensively via numerical simulations, but most previous simulations set the Prandtl number $Pr$ to unity. In this study we build more than 200 numerical models of rotating convection in a spherical shell over a wide range of $Pr$ ($10^{-2}\le Pr \le 10^2$). By increasing the Rayleigh number $Ra$, we characterise four different flow regimes, starting from the linear onset to multiple modes, then transitioning to the geostrophic turbulence and eventually approaching the weakly rotating regime. In the multiple modes regime, we show evidence of triadic resonances in numerical models with different $Pr$, which may provide a generic mechanism for the transition from laminar to turbulence in rotating convection. We analyse scaling behaviours of the heat transfer and convective flow speeds in numerical simulations, paying particular attention to the $Pr$ dependence. We find that the so-called diffusion-free scaling for the heat transfer cannot reconcile all numerical models with different $Pr$ in the geostrophic turbulence regime. However, the characteristic flow speeds at different $Pr$ roughly follow a unified scaling that can be described by visco-Archimedean–Coriolis force balances, though the scaling tends to approach the Coriolis-inertial-Archimedean force balance at low $Pr$. We also show that transition behaviours from rotating to non-rotating convection depend on $Pr$. The transition criteria based on heat transfer and flow morphology would be rather different when $Pr>1$, but the two criteria are consistent for cases with $Pr\le 1$. Both scaling behaviours and transition behaviours suggest that the heat transfer is controlled by the boundary layers while the convective flow speeds are mainly determined by the force balance in the bulk for cases with $Pr>1$, which is in line with recent experimental results with moderate to high $Pr$. For cases with $Pr \le 1$, both the heat transfer and convective velocities are approaching the inviscid dynamics in the bulk. We also briefly analysed the magnitude and scaling of zonal flows at different $Pr$, showing that the zonal flow amplitude rapidly increases as $Pr$ decreases.