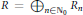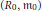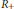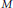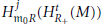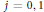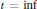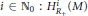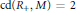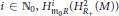1 results
Artinianness of Certain Graded Local Cohomology Modules
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 1 / 01 March 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 153-156
- Print publication:
- 01 March 2012
-
- Article
-
- You have access
- Export citation
-
We show that if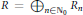
$R\,=\,{{\oplus }_{n\in \mathbb{N}0}}\,{{R}_{n}}$ is a Noetherian homogeneous ring with local base ring 
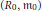$({{R}_{0}},\,{{m}_{0}})$, irrelevant ideal 
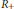${{R}_{+}}$, and 
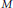$M$ a finitely generated graded 
$R$-module, then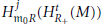 
$H_{{{m}_{0}}R}^{j}\,(H_{R+}^{t}\,(M))$ is Artinian for 
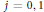$j\,=\,0,\,1$ where 
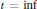$t\,=\,\inf ${
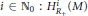$i\in {{\mathbb{N}}_{0}}:H_{R+}^{i}(M)$ is not finitely generated}. Also, we prove that if 
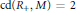$\text{cd(}{{R}_{+}},M)\,=\,2$, then for each 
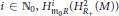$i\,\in \,{{\mathbb{N}}_{0}},\,H_{{{m}_{0}}R}^{i}\,(H_{R+}^{2}\,(M))$ is Artinian if and only if 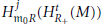$H_{{{m}_{0}}R}^{i+2}(H_{R+}^{1}(M))$ is Artinian, where 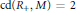$ \text{cd(}{{R}_{+}},\,M)$ is the cohomological dimension of $M$ with respect to ${{R}_{+}}$. This improves some results of R. Sazeedeh.
