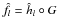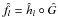This paper deals with the problem of estimating a regression function f,in a random design framework. We build and study two adaptive estimators based on modelselection, applied with warped bases. We start with a collection of finite dimensionallinear spaces, spanned by orthonormal bases. Instead of expanding directly the targetfunction f on these bases, we rather consider the expansion ofh = f ∘ G-1, whereG is the cumulative distribution function of the design, followingKerkyacharian and Picard [Bernoulli 10 (2004) 1053–1105].The data-driven selection of the (best) space is done with two strategies: we use both apenalization version of a “warped contrast”, and a model selection device in the spirit ofGoldenshluger and Lepski [Ann. Stat. 39 (2011) 1608–1632].We propose by these methods two functions, ĥl(l = 1, 2), easier to compute than least-squares estimators. Weestablish nonasymptotic mean-squared integrated risk bounds for the resulting estimators, \hbox{$\hat{f}_l=\hat{h}_l\circ G$}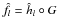f̂l = ĥl°G if G is known, or\hbox{$\hat{f}_l=\hat{h}_l\circ\hat{G}$}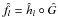f̂l = ĥl°Ĝ(l = 1,2) otherwise, where Ĝ is theempirical distribution function. We study also adaptive properties, in case the regressionfunction belongs to a Besov or Sobolev space, and compare the theoretical and practicalperformances of the two selection rules.

Our aim is to estimate the joint distribution of a finite sequence of independent categorical variables. We consider the collection of partitions into dyadic intervals and the associated histograms, and we select from the data the best histogram by minimizing a penalized least-squares criterion. The choice of the collection of partitions is inspired from approximation results due to DeVore and Yu. Our estimator satisfies a nonasymptotic oracle-type inequality and adaptivity properties in the minimax sense. Moreover, its computational complexity is only linear in the length of the sequence. We also use that estimator during the preliminary stage of a hybrid procedure for detecting multiple change-points in the joint distribution of the sequence. That second procedure still satisfies adaptivity properties and can be implemented efficiently. We provide a simulation study and apply the hybrid procedure to the segmentation of a DNA sequence.

In this paper a new approach for the formulation of the friction forces velocity function is introduced. The scope of this formulation is to facilitate the implementation of control laws for systems where friction forces appear. The friction model includes the exponential decay part, the Coulomb and viscous friction. The introduced formulation is based on the observation that the friction coefficient function of velocity can be presented as the solution of a linear differential equation. Due to this linearity, the parameters of the derived differential equation can be estimated easily by an adaptive system. The estimation of these parameters is equivalent to the estimation of the friction coefficient in the full range of operational velocities. This knowledge gives to the designed control systems the potential to avoid successfully the stick-slip phenomenon.

A control law for one D.O.F. system, where friction appears, is designed in order to prove the applicability of the proposed formulation of the friction model in control systems. A MRAC adaptive algorithm estimates the differential friction model parameters, using the measured friction force, while a sliding controller adjusts the motion of the mechanical system. The proposed friction model can be used in any control system where friction forces have to be compensated. The linear form of the model is suitable for common adaptive estimators. Therefore, the proposed structure is suitable for robotic applications, such as assembly, deburring, etc.