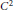1 results
Rectifiability of Optimal Transportation Plans
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 4 / 01 August 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 924-934
- Print publication:
- 01 August 2012
-
- Article
-
- You have access
- Export citation
-
The regularity of solutions to optimal transportation problems has become a hot topic in current research. It is well known by now that the optimal measure may not be concentrated on the graph of a continuous mapping unless both the transportation cost and the masses transported satisfy very restrictive hypotheses (including sign conditions on the mixed fourth-order derivatives of the cost function). The purpose of this note is to show that in spite of this, the optimal measure is supported on a Lipschitz manifold, provided only that the cost is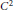
${{C}^{2}}$ with non-singular mixed second derivative. We use this result to provide a simple proof that solutions to Monge's optimal transportation problem satisfy a change of variables equation almost everywhere.
