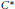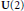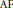The index theory considered in this paper, a generalisation of the classical Fredholm index theory, is obtained in terms of a non-finite trace on a unital 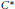${{C}^{*}}$-algebra. We relate it to the index theory of M. Breuer, which is developed in a von Neumann algebra setting, by means of a representation theorem. We show how our new index theory can be used to obtain an index theorem for Toeplitz operators on the compact group 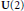$\text{U}\left( 2 \right)$, where the classical index theory does not give any interesting result.

We study the $\text{K}$-homology of the rotation algebras ${{A}_{\theta }}$ using the six-term cyclic sequence for the $\text{K}$-homology of a crossed product by $Z$. In the case that $\theta $ is irrational, we use Pimsner and Voiculescu's work on $\text{AF}$-embeddings of the ${{A}_{\theta }}$ to search for the missing generator of the even $\text{K}$-homology.