We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let A and M be closed linear operators defined on a complex Banach space X and let a ∈ L1(ℝ+) be a scalar kernel. We use operator-valued Fourier multipliers techniques to obtain necessary and sufficient conditions to guarantee the existence and uniqueness of periodic solutions to the equation
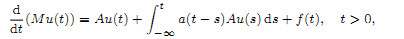
with initial condition Mu(0) = Mu(2π), solely in terms of spectral properties of the data. Our results are obtained in the scales of periodic Besov, Triebel–Lizorkin and Lebesgue vector-valued function spaces.
