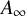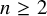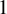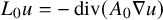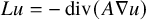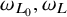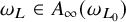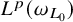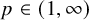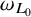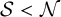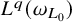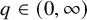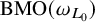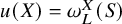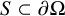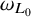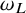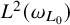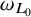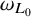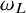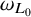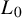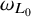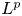Let
 $\Omega \subset \mathbb {R}^{n+1}$
,
$\Omega \subset \mathbb {R}^{n+1}$
,
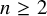 $n\ge 2$
, be a
$n\ge 2$
, be a
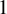 $1$
-sided nontangentially accessible domain, that is, a set which is quantitatively open and path-connected. Assume also that
$1$
-sided nontangentially accessible domain, that is, a set which is quantitatively open and path-connected. Assume also that
 $\Omega $
satisfies the capacity density condition. Let
$\Omega $
satisfies the capacity density condition. Let
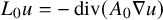 $L_0 u=-\mathop {\operatorname {div}}\nolimits (A_0 \nabla u)$
,
$L_0 u=-\mathop {\operatorname {div}}\nolimits (A_0 \nabla u)$
,
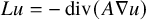 $Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
be two real (not necessarily symmetric) uniformly elliptic operators in
$Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
be two real (not necessarily symmetric) uniformly elliptic operators in
 $\Omega $
, and write
$\Omega $
, and write
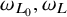 $\omega _{L_0}, \omega _L$
for the respective associated elliptic measures. We establish the equivalence between the following properties: (i)
$\omega _{L_0}, \omega _L$
for the respective associated elliptic measures. We establish the equivalence between the following properties: (i)
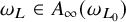 $\omega _L \in A_{\infty }(\omega _{L_0})$
, (ii) L is
$\omega _L \in A_{\infty }(\omega _{L_0})$
, (ii) L is
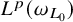 $L^p(\omega _{L_0})$
-solvable for some
$L^p(\omega _{L_0})$
-solvable for some
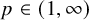 $p\in (1,\infty )$
, (iii) bounded null solutions of L satisfy Carleson measure estimates with respect to
$p\in (1,\infty )$
, (iii) bounded null solutions of L satisfy Carleson measure estimates with respect to
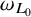 $\omega _{L_0}$
, (iv)
$\omega _{L_0}$
, (iv)
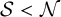 $\mathcal {S}<\mathcal {N}$
(i.e., the conical square function is controlled by the nontangential maximal function) in
$\mathcal {S}<\mathcal {N}$
(i.e., the conical square function is controlled by the nontangential maximal function) in
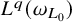 $L^q(\omega _{L_0})$
for some (or for all)
$L^q(\omega _{L_0})$
for some (or for all)
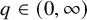 $q\in (0,\infty )$
for any null solution of L, and (v) L is
$q\in (0,\infty )$
for any null solution of L, and (v) L is
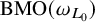 $\mathrm {BMO}(\omega _{L_0})$
-solvable. Moreover, in each of the properties (ii)-(v) it is enough to consider the class of solutions given by characteristic functions of Borel sets (i.e,
$\mathrm {BMO}(\omega _{L_0})$
-solvable. Moreover, in each of the properties (ii)-(v) it is enough to consider the class of solutions given by characteristic functions of Borel sets (i.e,
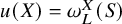 $u(X)=\omega _L^X(S)$
for an arbitrary Borel set
$u(X)=\omega _L^X(S)$
for an arbitrary Borel set
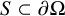 $S\subset \partial \Omega $
).
$S\subset \partial \Omega $
).
Also, we obtain a qualitative analog of the previous equivalences. Namely, we characterize the absolute continuity of
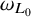 $\omega _{L_0}$
with respect to
$\omega _{L_0}$
with respect to
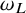 $\omega _L$
in terms of some qualitative local
$\omega _L$
in terms of some qualitative local
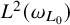 $L^2(\omega _{L_0})$
estimates for the truncated conical square function for any bounded null solution of L. This is also equivalent to the finiteness
$L^2(\omega _{L_0})$
estimates for the truncated conical square function for any bounded null solution of L. This is also equivalent to the finiteness
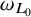 $\omega _{L_0}$
-almost everywhere of the truncated conical square function for any bounded null solution of L. As applications, we show that
$\omega _{L_0}$
-almost everywhere of the truncated conical square function for any bounded null solution of L. As applications, we show that
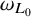 $\omega _{L_0}$
is absolutely continuous with respect to
$\omega _{L_0}$
is absolutely continuous with respect to
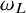 $\omega _L$
if the disagreement of the coefficients satisfies some qualitative quadratic estimate in truncated cones for
$\omega _L$
if the disagreement of the coefficients satisfies some qualitative quadratic estimate in truncated cones for
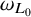 $\omega _{L_0}$
-almost everywhere vertex. Finally, when
$\omega _{L_0}$
-almost everywhere vertex. Finally, when
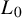 $L_0$
is either the transpose of L or its symmetric part, we obtain the corresponding absolute continuity upon assuming that the antisymmetric part of the coefficients has some controlled oscillation in truncated cones for
$L_0$
is either the transpose of L or its symmetric part, we obtain the corresponding absolute continuity upon assuming that the antisymmetric part of the coefficients has some controlled oscillation in truncated cones for
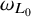 $\omega _{L_0}$
-almost every vertex.
$\omega _{L_0}$
-almost every vertex.
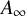 $A_{\infty }$
condition for elliptic operators in 1-sided nontangentially accessible domains satisfying the capacity density condition
$A_{\infty }$
condition for elliptic operators in 1-sided nontangentially accessible domains satisfying the capacity density condition