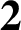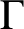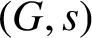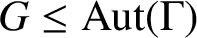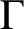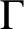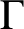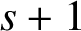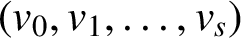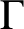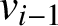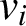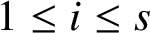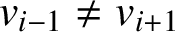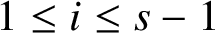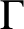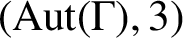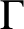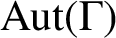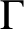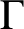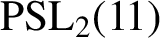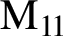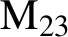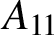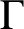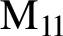A graph
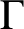 $\Gamma $
is called
$\Gamma $
is called
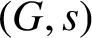 $(G, s)$
-arc-transitive if
$(G, s)$
-arc-transitive if
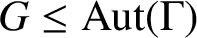 $G \le \text{Aut} (\Gamma )$
is transitive on the set of vertices of
$G \le \text{Aut} (\Gamma )$
is transitive on the set of vertices of
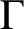 $\Gamma $
and the set of s-arcs of
$\Gamma $
and the set of s-arcs of
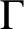 $\Gamma $
, where for an integer
$\Gamma $
, where for an integer
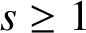 $s \ge 1$
an s-arc of
$s \ge 1$
an s-arc of
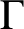 $\Gamma $
is a sequence of
$\Gamma $
is a sequence of
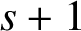 $s+1$
vertices
$s+1$
vertices
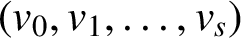 $(v_0,v_1,\ldots ,v_s)$
of
$(v_0,v_1,\ldots ,v_s)$
of
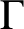 $\Gamma $
such that
$\Gamma $
such that
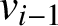 $v_{i-1}$
and
$v_{i-1}$
and
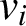 $v_i$
are adjacent for
$v_i$
are adjacent for
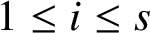 $1 \le i \le s$
and
$1 \le i \le s$
and
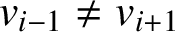 $v_{i-1}\ne v_{i+1}$
for
$v_{i-1}\ne v_{i+1}$
for
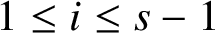 $1 \le i \le s-1$
. A graph
$1 \le i \le s-1$
. A graph
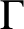 $\Gamma $
is called 2-transitive if it is
$\Gamma $
is called 2-transitive if it is
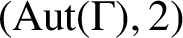 $(\text{Aut} (\Gamma ), 2)$
-arc-transitive but not
$(\text{Aut} (\Gamma ), 2)$
-arc-transitive but not
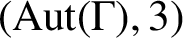 $(\text{Aut} (\Gamma ), 3)$
-arc-transitive. A Cayley graph
$(\text{Aut} (\Gamma ), 3)$
-arc-transitive. A Cayley graph
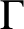 $\Gamma $
of a group G is called normal if G is normal in
$\Gamma $
of a group G is called normal if G is normal in
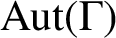 $\text{Aut} (\Gamma )$
and nonnormal otherwise. Fang et al. [‘On edge transitive Cayley graphs of valency four’, European J. Combin.25 (2004), 1103–1116] proved that if
$\text{Aut} (\Gamma )$
and nonnormal otherwise. Fang et al. [‘On edge transitive Cayley graphs of valency four’, European J. Combin.25 (2004), 1103–1116] proved that if
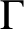 $\Gamma $
is a tetravalent 2-transitive Cayley graph of a finite simple group G, then either
$\Gamma $
is a tetravalent 2-transitive Cayley graph of a finite simple group G, then either
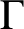 $\Gamma $
is normal or G is one of the groups
$\Gamma $
is normal or G is one of the groups
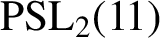 $\text{PSL}_2(11)$
,
$\text{PSL}_2(11)$
,
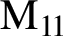 ${\rm M} _{11}$
,
${\rm M} _{11}$
,
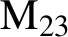 $\text{M} _{23}$
and
$\text{M} _{23}$
and
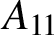 $A_{11}$
. However, it was unknown whether
$A_{11}$
. However, it was unknown whether
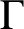 $\Gamma $
is normal when G is one of these four groups. We answer this question by proving that among these four groups only
$\Gamma $
is normal when G is one of these four groups. We answer this question by proving that among these four groups only
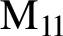 $\text{M} _{11}$
produces connected tetravalent 2-transitive nonnormal Cayley graphs. We prove further that there are exactly two such graphs which are nonisomorphic and both are determined in the paper. As a consequence, the automorphism group of any connected tetravalent 2-transitive Cayley graph of any finite simple group is determined.
$\text{M} _{11}$
produces connected tetravalent 2-transitive nonnormal Cayley graphs. We prove further that there are exactly two such graphs which are nonisomorphic and both are determined in the paper. As a consequence, the automorphism group of any connected tetravalent 2-transitive Cayley graph of any finite simple group is determined.
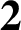 $\textbf{2}$
-TRANSITIVE NONNORMAL CAYLEY GRAPHS OF FINITE SIMPLE GROUPS
$\textbf{2}$
-TRANSITIVE NONNORMAL CAYLEY GRAPHS OF FINITE SIMPLE GROUPS