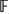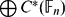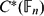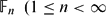Wick polynomials and Wick products are studied in the context of noncommutative probability theory. It is shown that free, Boolean, and conditionally free Wick polynomials can be defined and related through the action of the group of characters over a particular Hopf algebra. These results generalize our previous developments of a Hopf-algebraic approach to cumulants and Wick products in classical probability theory.

Incidence coalgebras of categories in the sense of Joni and Rota are studied, specifically cases where a monoidal product on the category turns these into (weak) bialgebras. The overlap with the theory of combinatorial Hopf algebras and that of Hopf quivers is discussed, and examples including trees, skew shapes, Milner’s bigraphs and crossed modules are considered.

Leti ${\Bbb F}$n be the free group of rank n and let $\bigoplus C^{*}({\Bbb F}_{n})$ denote the direct sum of full group C*-algebras $C^{*}({\Bbb F}_{n})$ of ${\Bbb F}_{n} (1\leq n<\infty$). We introduce a new comultiplication Δϕ on $\bigoplus C^{*}({\Bbb F}_{n})$ such that $(\bigoplus C^{*}({\Bbb F}_{n}),\,\Delta_{\varphi})$ is a non-cocommutative C*-bialgebra. With respect to Δϕ, the tensor product π⊗ϕπ′ of any two representations π and π′ of free groups is defined. The operation ×ϕ is associative and non-commutative. We compute its tensor product formulas of several representations.

Let A ⊆ E be an extension of Hopf algebras such that there exists a normal left A-module coalgebra map π : E → A that splits the inclusion. We shall describe the set of all coquasitriangular structures on the Hopf algebra E in terms of the datum (A, E, π) as follows: first, any such extension E is isomorphic to a unified product A ⋉ H, for some unitary subcoalgebra H of E (A. L. Agore and G. Militaru, Unified products and split extensions of Hopf algebras, to appear in AMS Contemp. Math.). Then, as a main theorem, we establish a bijective correspondence between the set of all coquasitriangular structures on an arbitrary unified product A ⋉ H and a certain set of datum (p, τ, u, v) related to the components of the unified product. As the main application, we derive necessary and sufficient conditions for Majid's infinite-dimensional quantum double Dλ(A, H) = A ⋈τH to be a coquasitriangular Hopf algebra. Several examples are worked out in detail.