There is an extensive body of literature on the bicyclic biquadratic fields. These fields provide the simplest examples of abelian noncyclic extensions of Q. In sharp contrast, there is a dearth of literature on the bicyclic bicubic extensions of the rational numbers. These fields together with the abelian noncyclic octic extensions provide the next simplest abelian noncyclic extensions.

In this article, we shall study abelian bicyclic bicubic extensions of Q of degree 9. Hasse [4, v-ix] has stated as important objectives: the computation of an integral basis, the determination of class number and the calculation of fundamental units for abelian fields. In this article, we will solve the first problem completely, and show that the solution to the unit problem leads to a solution of the class number problem. Moreover, we shall give a method for determining the unit group up to a subgroup which has index 1 or 3 and so determine the class number up to a factor of 3.

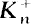Let n ≥3 and m≥3 be integers. Let Kn be the cyclotomic field obtained by adjoining a primitive nth root of unity to the field of rational numbers. Let denote the maximal real subfield of 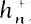Kn. Let hn (resp., ) denote the class number of 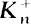Kn (resp., ). For fixed 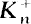m we show that m divides hn and hn for asymptotically almost all n. 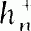Also for those Kn and with a given number of ramified primes, we obtain lower bounds for certain types of densities for m dividing hn and .

Let h(m) denote the class number of the quadratic field Q(√m). In this paper necessary and sufficient conditions for h (m) to be divisible by 16 are determined when m = −p, where p is a prime congruent to 1 modulo 8, and when m = −2p, where p is a prime congruent to ±1 modulo 8.