1 results
Finite Clones Containing All Permutations
-
- Journal:
- Canadian Journal of Mathematics / Volume 46 / Issue 5 / 01 October 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 951-970
- Print publication:
- 01 October 1994
-
- Article
-
- You have access
- Export citation
-
Let A be a finite set with |A| > 2. We describe all clones on A containing the set SA of all permutations of A among its unary operations. (A clone on A is a composition closed set of finitary operations on A containing all projections). With a few exceptions such a clone C is either essentially unary or cellular i.e. there exists a monoid M of self-maps of A containing SA such that either C =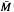
(= all essentially unary operations agreeing with some f ∊ M) or C = 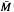∪ Гh where 1 < h ≤ |A| and Гh consists of all finitary operations on A taking at most h values. The exceptions are subclones of Burle's clone or of its variant (provided |A| is even).
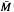(= all essentially unary operations agreeing with some 