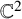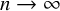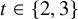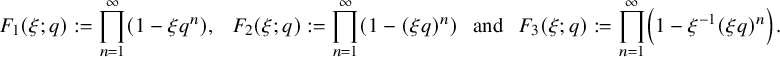Recent works at the interface of algebraic combinatorics, algebraic geometry, number theory and topology have provided new integer-valued invariants on integer partitions. It is natural to consider the distribution of partitions when sorted by these invariants in congruence classes. We consider the prominent situations that arise from extensions of the Nekrasov–Okounkov hook product formula and from Betti numbers of various Hilbert schemes of n points on
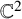 ${\mathbb {C}}^2$
. For the Hilbert schemes, we prove that homology is equidistributed as
${\mathbb {C}}^2$
. For the Hilbert schemes, we prove that homology is equidistributed as
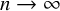 $n\to \infty $
. For t-hooks, we prove distributions that are often not equidistributed. The cases where
$n\to \infty $
. For t-hooks, we prove distributions that are often not equidistributed. The cases where
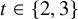 $t\in \{2, 3\}$
stand out, as there are congruence classes where such counts are zero. To obtain these distributions, we obtain analytic results of independent interest. We determine the asymptotics, near roots of unity, of the ubiquitous infinite products
$t\in \{2, 3\}$
stand out, as there are congruence classes where such counts are zero. To obtain these distributions, we obtain analytic results of independent interest. We determine the asymptotics, near roots of unity, of the ubiquitous infinite products
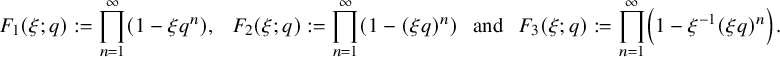 $$ \begin{align*}F_1(\xi; q):=\prod_{n=1}^{\infty}\left(1-\xi q^n\right), \ \ \ F_2(\xi; q):=\prod_{n=1}^{\infty}\left(1-(\xi q)^n\right) \ \ \ {\mathrm{and}}\ \ \ F_3(\xi; q):=\prod_{n=1}^{\infty}\left(1-\xi^{-1}(\xi q)^n\right). \end{align*} $$
$$ \begin{align*}F_1(\xi; q):=\prod_{n=1}^{\infty}\left(1-\xi q^n\right), \ \ \ F_2(\xi; q):=\prod_{n=1}^{\infty}\left(1-(\xi q)^n\right) \ \ \ {\mathrm{and}}\ \ \ F_3(\xi; q):=\prod_{n=1}^{\infty}\left(1-\xi^{-1}(\xi q)^n\right). \end{align*} $$